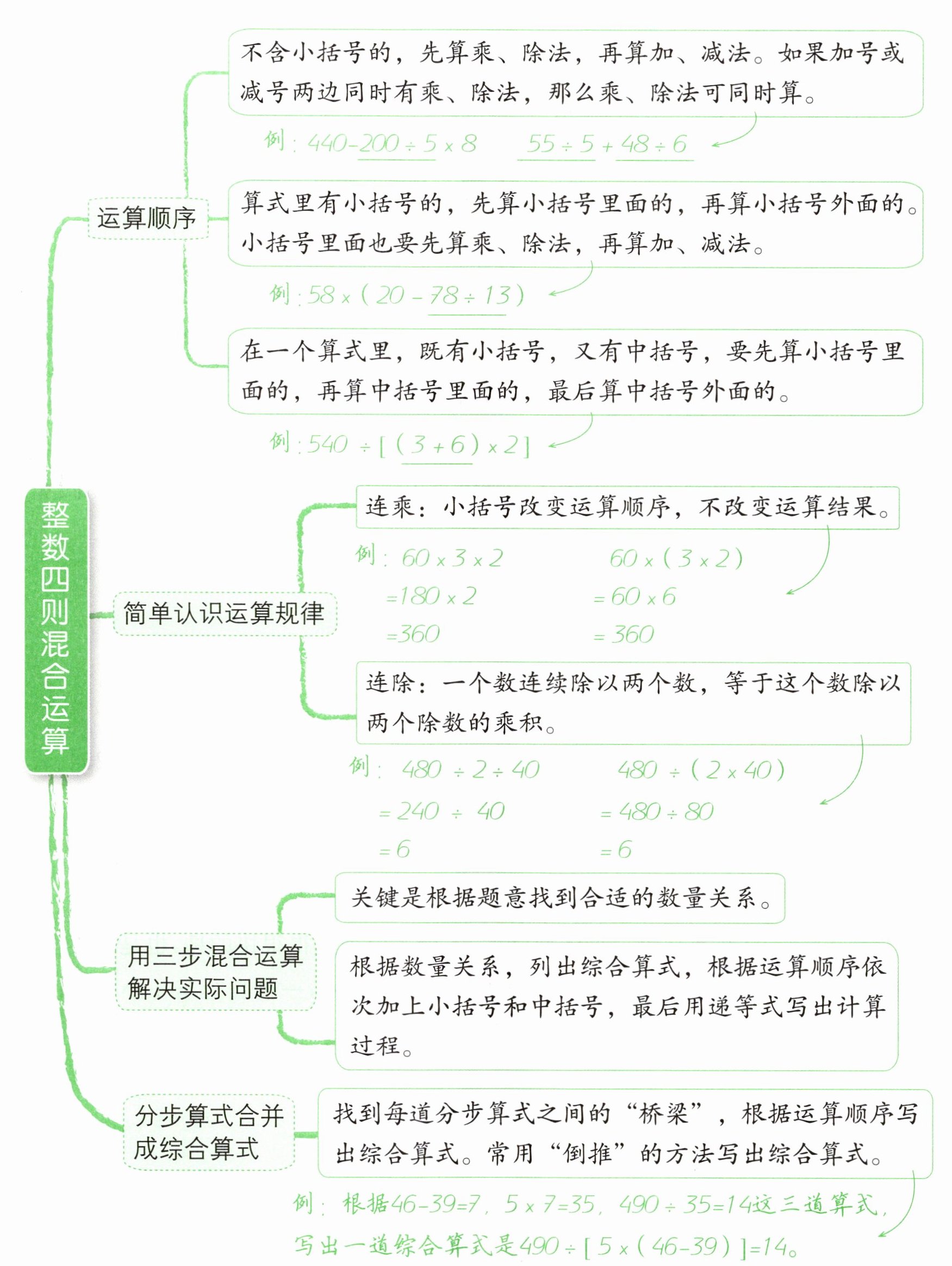
- 不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。
例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案:
整数四则混合运算知识梳理
一、运算顺序
1. 不含小括号
先算乘、除法,再算加、减法。
加号或减号两边同时有乘、除法,乘、除法可同时算。
例:
$440 - 200 ÷ 5 × 8$
$= 440 - 40 × 8$
$= 440 - 320$
$= 120$
$55 ÷ 5 + 48 ÷ 6$
$= 11 + 8$
$= 19$
2. 含小括号
先算小括号里面的,再算小括号外面的;小括号内先算乘、除法,再算加、减法。
例:
$58 × (20 - 78 ÷ 13)$
$= 58 × (20 - 6)$
$= 58 × 14$
$= 812$
3. 含小括号和中括号
先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:
$540 ÷ [(3 + 6) × 2]$
$= 540 ÷ [9 × 2]$
$= 540 ÷ 18$
$= 30$
二、简单认识运算规律
1. 连乘
小括号改变运算顺序,不改变运算结果。
例:
$60 × 3 × 2 = 180 × 2 = 360$
$60 × (3 × 2) = 60 × 6 = 360$
2. 连除
一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:
$480 ÷ 2 ÷ 40 = 240 ÷ 40 = 6$
$480 ÷ (2 × 40) = 480 ÷ 80 = 6$
三、用三步混合运算解决实际问题
步骤:找数量关系→列综合算式(加括号)→递等式计算。
四、分步算式合并成综合算式
方法:找“桥梁”,用“倒推”法,按运算顺序加括号。
例:
分步算式:$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$
综合算式:$490 ÷ [5 × (46 - 39)] = 14$
一、运算顺序
1. 不含小括号
先算乘、除法,再算加、减法。
加号或减号两边同时有乘、除法,乘、除法可同时算。
例:
$440 - 200 ÷ 5 × 8$
$= 440 - 40 × 8$
$= 440 - 320$
$= 120$
$55 ÷ 5 + 48 ÷ 6$
$= 11 + 8$
$= 19$
2. 含小括号
先算小括号里面的,再算小括号外面的;小括号内先算乘、除法,再算加、减法。
例:
$58 × (20 - 78 ÷ 13)$
$= 58 × (20 - 6)$
$= 58 × 14$
$= 812$
3. 含小括号和中括号
先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:
$540 ÷ [(3 + 6) × 2]$
$= 540 ÷ [9 × 2]$
$= 540 ÷ 18$
$= 30$
二、简单认识运算规律
1. 连乘
小括号改变运算顺序,不改变运算结果。
例:
$60 × 3 × 2 = 180 × 2 = 360$
$60 × (3 × 2) = 60 × 6 = 360$
2. 连除
一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:
$480 ÷ 2 ÷ 40 = 240 ÷ 40 = 6$
$480 ÷ (2 × 40) = 480 ÷ 80 = 6$
三、用三步混合运算解决实际问题
步骤:找数量关系→列综合算式(加括号)→递等式计算。
四、分步算式合并成综合算式
方法:找“桥梁”,用“倒推”法,按运算顺序加括号。
例:
分步算式:$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$
综合算式:$490 ÷ [5 × (46 - 39)] = 14$
- 不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案:
解析:本题考查的知识点是整数四则混合运算,包括运算顺序、运算规律、用三步混合运算解决实际问题以及分步算式合并成综合算式。
1. 运算顺序:
不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
2. 运算规律:
连乘:小括号改变运算顺序,不改变运算结果。
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
3. 用三步混合运算解决实际问题:关键是根据题意找到合适的数量关系,根据数量关系列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
4. 分步算式合并成综合算式:找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
答案:
1. 运算顺序:
$440 - 200÷ 5× 8$
$= 440 - 40× 8$
$= 440 - 320$
$= 120$
$55÷ 5 + 48÷ 6$
$= 11 + 8$
$= 19$
$58×(20 - 78÷ 13)$
$= 58×(20 - 6)$
$= 58× 14$
$= 812$
$540÷[(3 + 6)× 2]$
$= 540÷(9× 2)$
$= 540÷ 18$
$= 30$
2. 运算规律:
$60× 3× 2$
$= 180× 2$
$= 360$
$60×(3× 2)$
$= 60× 6$
$= 360$
$480÷ 2÷ 40$
$= 240÷ 40$
$= 6$
$480÷(2× 40)$
$= 480÷ 80$
$= 6$
3. 用三步混合运算解决实际问题:根据具体题目找数量关系列综合算式计算。
4. 分步算式合并成综合算式:
根据$46 - 39 = 7$,$5× 7 = 35$,$490÷ 35 = 14$,综合算式是$490÷[5×(46 - 39)] = 14$。
1. 运算顺序:
不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
2. 运算规律:
连乘:小括号改变运算顺序,不改变运算结果。
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
3. 用三步混合运算解决实际问题:关键是根据题意找到合适的数量关系,根据数量关系列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
4. 分步算式合并成综合算式:找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
答案:
1. 运算顺序:
$440 - 200÷ 5× 8$
$= 440 - 40× 8$
$= 440 - 320$
$= 120$
$55÷ 5 + 48÷ 6$
$= 11 + 8$
$= 19$
$58×(20 - 78÷ 13)$
$= 58×(20 - 6)$
$= 58× 14$
$= 812$
$540÷[(3 + 6)× 2]$
$= 540÷(9× 2)$
$= 540÷ 18$
$= 30$
2. 运算规律:
$60× 3× 2$
$= 180× 2$
$= 360$
$60×(3× 2)$
$= 60× 6$
$= 360$
$480÷ 2÷ 40$
$= 240÷ 40$
$= 6$
$480÷(2× 40)$
$= 480÷ 80$
$= 6$
3. 用三步混合运算解决实际问题:根据具体题目找数量关系列综合算式计算。
4. 分步算式合并成综合算式:
根据$46 - 39 = 7$,$5× 7 = 35$,$490÷ 35 = 14$,综合算式是$490÷[5×(46 - 39)] = 14$。
- 不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案:
整数四则混合运算知识梳理
一、运算顺序
1. 不含小括号
先算乘、除法,再算加、减法。
加号或减号两边同时有乘、除法,乘、除法可同时算。
例:
$440 - 200 ÷ 5 × 8$
$= 440 - 40 × 8$
$= 440 - 320$
$= 120$
$55 ÷ 5 + 48 ÷ 6$
$= 11 + 8$
$= 19$
2. 含小括号
先算小括号里面的,再算小括号外面的;小括号内先算乘、除法,再算加、减法。
例:
$58 × (20 - 78 ÷ 13)$
$= 58 × (20 - 6)$
$= 58 × 14$
$= 812$
3. 含小括号和中括号
先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:
$540 ÷ [(3 + 6) × 2]$
$= 540 ÷ [9 × 2]$
$= 540 ÷ 18$
$= 30$
二、简单认识运算规律
1. 连乘
小括号改变运算顺序,不改变运算结果。
例:
$60 × 3 × 2 = 180 × 2 = 360$
$60 × (3 × 2) = 60 × 6 = 360$
2. 连除
一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:
$480 ÷ 2 ÷ 40 = 240 ÷ 40 = 6$
$480 ÷ (2 × 40) = 480 ÷ 80 = 6$
三、用三步混合运算解决实际问题
关键:找数量关系,列综合算式,按运算顺序加括号,递等式计算。
四、分步算式合并成综合算式
方法:找“桥梁”,用“倒推”法,按运算顺序加括号。
例:
分步算式:$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$
综合算式:$490 ÷ [5 × (46 - 39)] = 14$
一、运算顺序
1. 不含小括号
先算乘、除法,再算加、减法。
加号或减号两边同时有乘、除法,乘、除法可同时算。
例:
$440 - 200 ÷ 5 × 8$
$= 440 - 40 × 8$
$= 440 - 320$
$= 120$
$55 ÷ 5 + 48 ÷ 6$
$= 11 + 8$
$= 19$
2. 含小括号
先算小括号里面的,再算小括号外面的;小括号内先算乘、除法,再算加、减法。
例:
$58 × (20 - 78 ÷ 13)$
$= 58 × (20 - 6)$
$= 58 × 14$
$= 812$
3. 含小括号和中括号
先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:
$540 ÷ [(3 + 6) × 2]$
$= 540 ÷ [9 × 2]$
$= 540 ÷ 18$
$= 30$
二、简单认识运算规律
1. 连乘
小括号改变运算顺序,不改变运算结果。
例:
$60 × 3 × 2 = 180 × 2 = 360$
$60 × (3 × 2) = 60 × 6 = 360$
2. 连除
一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:
$480 ÷ 2 ÷ 40 = 240 ÷ 40 = 6$
$480 ÷ (2 × 40) = 480 ÷ 80 = 6$
三、用三步混合运算解决实际问题
关键:找数量关系,列综合算式,按运算顺序加括号,递等式计算。
四、分步算式合并成综合算式
方法:找“桥梁”,用“倒推”法,按运算顺序加括号。
例:
分步算式:$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$
综合算式:$490 ÷ [5 × (46 - 39)] = 14$
- 不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案:
解析:本题考查的知识点是四则混合运算的运算顺序、运算规律以及用三步混合运算解决实际问题、分步算式合并成综合算式等知识点。
四则混合运算顺序:不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算;算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法;在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
连乘:小括号改变运算顺序,不改变运算结果;连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
用三步混合运算解决实际问题的关键是根据题意找到合适的数量关系,根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式要找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
答案:
1.四则混合运算顺序:
不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$
$=440 - 40 × 8$
$=440 - 320$
$=120$
$55 ÷ 5 + 48 ÷ 6$
$=11 + 8$
$=19$
算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
$=58 × (20 - 6)$
$=58 × 14$
$=812$
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
$=540 ÷ [9 × 2]$
$=540 ÷ 18$
$=30$
2.简单认识运算规律:
连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$
$=180 × 2$
$=360$
$60 × (3 × 2)$
$=60 × 6$
$=360$
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$
$=240 ÷ 40$
$=6$
$480 ÷ (2 × 40)$
$=480 ÷ 80$
$=6$
3.用三步混合运算解决实际问题:关键是根据题意找到合适的数量关系,根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
4.分步算式合并成综合算式:找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。
四则混合运算顺序:不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算;算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法;在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
连乘:小括号改变运算顺序,不改变运算结果;连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
用三步混合运算解决实际问题的关键是根据题意找到合适的数量关系,根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式要找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
答案:
1.四则混合运算顺序:
不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$
$=440 - 40 × 8$
$=440 - 320$
$=120$
$55 ÷ 5 + 48 ÷ 6$
$=11 + 8$
$=19$
算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
$=58 × (20 - 6)$
$=58 × 14$
$=812$
在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
$=540 ÷ [9 × 2]$
$=540 ÷ 18$
$=30$
2.简单认识运算规律:
连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$
$=180 × 2$
$=360$
$60 × (3 × 2)$
$=60 × 6$
$=360$
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$
$=240 ÷ 40$
$=6$
$480 ÷ (2 × 40)$
$=480 ÷ 80$
$=6$
3.用三步混合运算解决实际问题:关键是根据题意找到合适的数量关系,根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
4.分步算式合并成综合算式:找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。
- 不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案:
整数四则混合运算知识梳理
1. 运算顺序
不含小括号:先算乘、除法,再算加、减法;加号或减号两边同时有乘、除法,乘、除法可同时算。
例:$440-200÷5×8$;$55÷5+48÷6$
含小括号:先算小括号里面的(小括号内先算乘、除法,再算加、减法),再算小括号外面的。
例:$58×(20-78÷13)$
含小括号和中括号:先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540÷[(3+6)×2]$
2. 简单认识运算规律
连乘:小括号改变运算顺序,不改变运算结果。
例:$60×3×2=360$;$60×(3×2)=360$
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480÷2÷40=6$;$480÷(2×40)=6$
3. 用三步混合运算解决实际问题
关键:找到合适的数量关系。
步骤:根据数量关系列综合算式,按运算顺序加小括号和中括号,用递等式计算。
4. 分步算式合并成综合算式
方法:找分步算式间的“桥梁”,用“倒推”法,按运算顺序写综合算式。
例:根据$46-39=7$,$5×7=35$,$490÷35=14$,综合算式为$490÷[5×(46-39)]=14$。
1. 运算顺序
不含小括号:先算乘、除法,再算加、减法;加号或减号两边同时有乘、除法,乘、除法可同时算。
例:$440-200÷5×8$;$55÷5+48÷6$
含小括号:先算小括号里面的(小括号内先算乘、除法,再算加、减法),再算小括号外面的。
例:$58×(20-78÷13)$
含小括号和中括号:先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540÷[(3+6)×2]$
2. 简单认识运算规律
连乘:小括号改变运算顺序,不改变运算结果。
例:$60×3×2=360$;$60×(3×2)=360$
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480÷2÷40=6$;$480÷(2×40)=6$
3. 用三步混合运算解决实际问题
关键:找到合适的数量关系。
步骤:根据数量关系列综合算式,按运算顺序加小括号和中括号,用递等式计算。
4. 分步算式合并成综合算式
方法:找分步算式间的“桥梁”,用“倒推”法,按运算顺序写综合算式。
例:根据$46-39=7$,$5×7=35$,$490÷35=14$,综合算式为$490÷[5×(46-39)]=14$。
- 不含小括号的,先算乘、除法,再算加、减法。如果加号或减号两边同时有乘、除法,那么乘、除法可同时算。
例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

例:$440 - 200 ÷ 5 × 8$ $55 ÷ 5 + 48 ÷ 6$
- 算式里有小括号的,先算小括号里面的,再算小括号外面的。小括号里面也要先算乘、除法,再算加、减法。
例:$58 × (20 - 78 ÷ 13)$
- 在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540 ÷ [(3 + 6) × 2]$
简单认识运算规律
- 连乘:小括号改变运算顺序,不改变运算结果。
例:$60 × 3 × 2$ $60 × (3 × 2)$
$=180 × 2$ $=60 × 6$
$=360$ $=360$
- 连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480 ÷ 2 ÷ 40$ $480 ÷ (2 × 40)$
$=240 ÷ 40$ $=480 ÷ 80$
$=6$ $=6$
用三步混合运算解决实际问题
- 关键是根据题意找到合适的数量关系。
- 根据数量关系,列出综合算式,根据运算顺序依次加上小括号和中括号,最后用递等式写出计算过程。
分步算式合并成综合算式
- 找到每道分步算式之间的“桥梁”,根据运算顺序写出综合算式。常用“倒推”的方法写出综合算式。
例:根据$46 - 39 = 7$,$5 × 7 = 35$,$490 ÷ 35 = 14$这三道算式,写出一道综合算式是$490 ÷ [5 × (46 - 39)] = 14$。

答案:
整数四则混合运算
1. 运算顺序
不含小括号:先算乘、除法,再算加、减法;加号或减号两边同时有乘、除法,乘、除法可同时算。
例:$440-200÷5×8$;$55÷5+48÷6$
含小括号:先算小括号里面的(括号内先算乘、除法,再算加、减法),再算小括号外面的。
例:$58×(20-78÷13)$
含小括号和中括号:先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540÷[(3+6)×2]$
2. 简单认识运算规律
连乘:小括号改变运算顺序,不改变运算结果。
例:$60×3×2=360$;$60×(3×2)=360$
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480÷2÷40=6$;$480÷(2×40)=6$
3. 用三步混合运算解决实际问题
关键:找数量关系,列综合算式,按运算顺序加括号,用递等式计算。
4. 分步算式合并成综合算式
方法:找“桥梁”,用“倒推”法,按运算顺序写综合算式。
例:由$46-39=7$,$5×7=35$,$490÷35=14$,得综合算式$490÷[5×(46-39)]=14$。
1. 运算顺序
不含小括号:先算乘、除法,再算加、减法;加号或减号两边同时有乘、除法,乘、除法可同时算。
例:$440-200÷5×8$;$55÷5+48÷6$
含小括号:先算小括号里面的(括号内先算乘、除法,再算加、减法),再算小括号外面的。
例:$58×(20-78÷13)$
含小括号和中括号:先算小括号里面的,再算中括号里面的,最后算中括号外面的。
例:$540÷[(3+6)×2]$
2. 简单认识运算规律
连乘:小括号改变运算顺序,不改变运算结果。
例:$60×3×2=360$;$60×(3×2)=360$
连除:一个数连续除以两个数,等于这个数除以两个除数的乘积。
例:$480÷2÷40=6$;$480÷(2×40)=6$
3. 用三步混合运算解决实际问题
关键:找数量关系,列综合算式,按运算顺序加括号,用递等式计算。
4. 分步算式合并成综合算式
方法:找“桥梁”,用“倒推”法,按运算顺序写综合算式。
例:由$46-39=7$,$5×7=35$,$490÷35=14$,得综合算式$490÷[5×(46-39)]=14$。
查看更多完整答案,请扫码查看


