理解题意:可以列表整理条件和问题。
分析数量关系:可以从条件出发,也可以从问题出发。
列式解答:过程完整、注意单位。
仔细检验:可以用不同方法再算一遍。也可以逆向求证。
问题模型
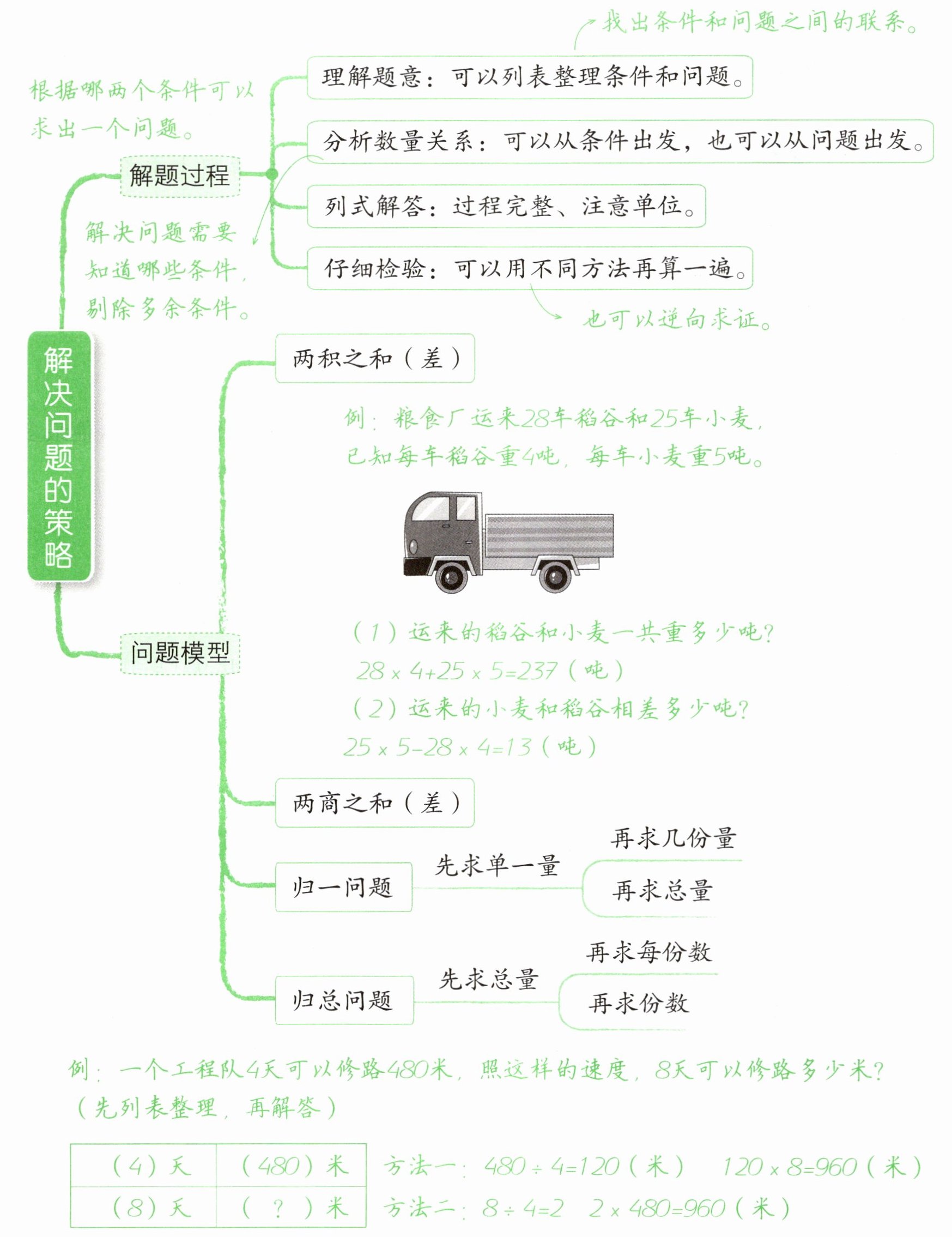
两积之和(差)
例:粮食厂运来28车稻谷和25车小麦,已知每车稻谷重4吨,每车小麦重5吨。
(1)运来的稻谷和小麦一共重多少吨?
28×4+25×5= 237(吨)
(2)运来的小麦和稻谷相差多少吨?
25×5-28×4= 13(吨)
两商之和(差)
归一问题:先求单一量 再求几份量 再求总量
归总问题:先求总量 再求每份数 再求份数
例:一个工程队4天可以修路480米,照这样的速度,8天可以修路多少米?(先列表整理,再解答)
|(4)天|(480)米|
|(8)天|(?)米|
方法一:480÷4= 120(米) 120×8= 960(米)
方法二:8÷4= 2 2×480= 960(米)
分析数量关系:可以从条件出发,也可以从问题出发。
列式解答:过程完整、注意单位。
仔细检验:可以用不同方法再算一遍。也可以逆向求证。
问题模型
两积之和(差)
例:粮食厂运来28车稻谷和25车小麦,已知每车稻谷重4吨,每车小麦重5吨。
(1)运来的稻谷和小麦一共重多少吨?
28×4+25×5= 237(吨)
(2)运来的小麦和稻谷相差多少吨?
25×5-28×4= 13(吨)
两商之和(差)
归一问题:先求单一量 再求几份量 再求总量
归总问题:先求总量 再求每份数 再求份数
例:一个工程队4天可以修路480米,照这样的速度,8天可以修路多少米?(先列表整理,再解答)
|(4)天|(480)米|
|(8)天|(?)米|
方法一:480÷4= 120(米) 120×8= 960(米)
方法二:8÷4= 2 2×480= 960(米)

答案:
解析:
本题主要考查了利用四则运算解决实际问题,关键在于理解题目中的数量关系,并根据不同的问题模型进行列式计算。
对于“两积之和(差)”问题,需要分别计算出两种事物的总量,再进行相应的加法或减法运算。
对于“两商之和(差)”中的归一和归总问题,归一问题是先求出单一量,再根据单一量求出其他量;归总问题是先求出总量,再根据总量求出其他相关量。
答案:
(1)运来的稻谷和小麦一共重$237$吨。
(2)运来的小麦和稻谷相差$13$吨。
一个工程队$4$天可以修路$480$米,照这样的速度,$8$天可以修路$960$米。
本题主要考查了利用四则运算解决实际问题,关键在于理解题目中的数量关系,并根据不同的问题模型进行列式计算。
对于“两积之和(差)”问题,需要分别计算出两种事物的总量,再进行相应的加法或减法运算。
对于“两商之和(差)”中的归一和归总问题,归一问题是先求出单一量,再根据单一量求出其他量;归总问题是先求出总量,再根据总量求出其他相关量。
答案:
(1)运来的稻谷和小麦一共重$237$吨。
(2)运来的小麦和稻谷相差$13$吨。
一个工程队$4$天可以修路$480$米,照这样的速度,$8$天可以修路$960$米。
理解题意:可以列表整理条件和问题。
分析数量关系:可以从条件出发,也可以从问题出发。
列式解答:过程完整、注意单位。
仔细检验:可以用不同方法再算一遍。也可以逆向求证。
问题模型
两积之和(差)
例:粮食厂运来28车稻谷和25车小麦,已知每车稻谷重4吨,每车小麦重5吨。
(1)运来的稻谷和小麦一共重多少吨?
28×4+25×5= 237(吨)
(2)运来的小麦和稻谷相差多少吨?
25×5-28×4= 13(吨)
两商之和(差)
归一问题:先求单一量 再求几份量 再求总量
归总问题:先求总量 再求每份数 再求份数
例:一个工程队4天可以修路480米,照这样的速度,8天可以修路多少米?(先列表整理,再解答)
|(4)天|(480)米|
|(8)天|(?)米|
方法一:480÷4= 120(米) 120×8= 960(米)
方法二:8÷4= 2 2×480= 960(米)

分析数量关系:可以从条件出发,也可以从问题出发。
列式解答:过程完整、注意单位。
仔细检验:可以用不同方法再算一遍。也可以逆向求证。
问题模型
两积之和(差)
例:粮食厂运来28车稻谷和25车小麦,已知每车稻谷重4吨,每车小麦重5吨。
(1)运来的稻谷和小麦一共重多少吨?
28×4+25×5= 237(吨)
(2)运来的小麦和稻谷相差多少吨?
25×5-28×4= 13(吨)
两商之和(差)
归一问题:先求单一量 再求几份量 再求总量
归总问题:先求总量 再求每份数 再求份数
例:一个工程队4天可以修路480米,照这样的速度,8天可以修路多少米?(先列表整理,再解答)
|(4)天|(480)米|
|(8)天|(?)米|
方法一:480÷4= 120(米) 120×8= 960(米)
方法二:8÷4= 2 2×480= 960(米)

答案:
解析:本题考查两积之和(差)、两商之和(差)、归一问题、归总问题等数量关系以及分析方法。
答案:
1.两积之和(差)
运来的稻谷和小麦一共重多少吨?
$28 × 4+25 × 5$
$=112 + 125$
$=237$(吨)
运来的小麦和稻谷相差多少吨?
$25 × 5-28 × 4$
$=125-112$
$=13$(吨)
2.两商之和(差)
3.归一问题
先求单一量:$480÷4 = 120$(米)
再求总量:$120×8 = 960$(米)
4.归总问题
先求总量:已知4天修480米,总量就是480米(这里求总量是为了通过它求每份数)。
再求每份数:$480÷4 = 120$(米/天)
再求份数:$120×8 = 960$(米)
综上,8天可以修路960米。
答案:
1.两积之和(差)
运来的稻谷和小麦一共重多少吨?
$28 × 4+25 × 5$
$=112 + 125$
$=237$(吨)
运来的小麦和稻谷相差多少吨?
$25 × 5-28 × 4$
$=125-112$
$=13$(吨)
2.两商之和(差)
3.归一问题
先求单一量:$480÷4 = 120$(米)
再求总量:$120×8 = 960$(米)
4.归总问题
先求总量:已知4天修480米,总量就是480米(这里求总量是为了通过它求每份数)。
再求每份数:$480÷4 = 120$(米/天)
再求份数:$120×8 = 960$(米)
综上,8天可以修路960米。
查看更多完整答案,请扫码查看


