《2025年人教金学典同步解析与测评五年级数学上册人教版云南专版》

探究$◯\!\!\!\!\,交流$
探究：在方格纸上用数对确定物体的位置。
卧佛寺公园示意图



人工湖$(4,2)$ 动物园$(6,5)$ 百鸟园$(6,4)$
1.用数对$(1,2)$表示西门的位置,你发现了什么?
方格纸上竖线与横线的任何一个交点都能用(数对)确定其位置。

2.比较西门和人工湖的位置,我发现：这两个景点位置的特点是(在同一行上)。
比较动物园和百鸟园的位置,我发现：这两个景点位置的特点是(在同一列上)。

答案： （2,5）（4,4）1.数对 2.在同一行上 在同一列上

1.游动物园,填位置。

(1)写出下面场馆的位置。
河马馆$(3,6)$ 海洋馆$(5,2)$
大象馆$(1,1)$ 猴山$(3,3)$
(2)在图上标出下面场馆的位置。
熊猫馆$(5,4)$ 猩猩馆$(2,4)$
虎山$(1,5)$
熊猫馆$(5,4)$：在横坐标为$5$，纵坐标为$4$的位置标记；猩猩馆$(2,4)$：在横坐标为$2$，纵坐标为$4$的位置标记；虎山$(1,5)$：在横坐标为$1$，纵坐标为$5$的位置标记。

答案： 1. （1）
河马馆$(3,6)$；
海洋馆$(5,2)$；
大象馆$(1,1)$；
猴山$(3,3)$。
2. （2）
熊猫馆$(5,4)$：在横坐标为$5$，纵坐标为$4$的位置标记；
猩猩馆$(2,4)$：在横坐标为$2$，纵坐标为$4$的位置标记；
虎山$(1,5)$：在横坐标为$1$，纵坐标为$5$的位置标记。

2.仔细观察下图,完成各题。

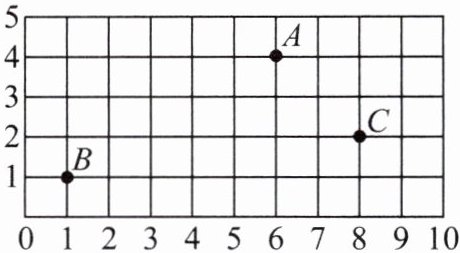
(1)照样子写出图中各点的位置。
$A(6,4)B$(1,1)$C$(8,2)
(2)先在图上标出点$D(2,3)$,$E(4,1)$,再顺次连接点$A$,$D$,$E$,$C$,$A$,看一看,围成的是什么图形?
平行四边形

答案： 1. （1）
根据数对的定义：数对是一个表示位置的概念，相当于坐标，前一个数字表示列，后一个数字表示行。
对于点$B$，它在第$1$列，第$1$行，所以$B(1,1)$；
对于点$C$，它在第$8$列，第$2$行，所以$C(8,2)$。
2. （2）
解：在图上标出$D(2,3)$，$E(4,1)$后，顺次连接$A(6,4)$，$D(2,3)$，$E(4,1)$，$C(8,2)$，$A(6,4)$。
我们可以通过计算线段的长度或者观察图形的形状来判断。
计算$AD$：根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$，$A(6,4)$，$D(2,3)$，$d_{AD}=\sqrt{(6 - 2)^2+(4 - 3)^2}=\sqrt{16 + 1}=\sqrt{17}$；
$DE$：$D(2,3)$，$E(4,1)$，$d_{DE}=\sqrt{(4 - 2)^2+(1 - 3)^2}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$；
$EC$：$E(4,1)$，$C(8,2)$，$d_{EC}=\sqrt{(8 - 4)^2+(2 - 1)^2}=\sqrt{16 + 1}=\sqrt{17}$；
$CA$：$C(8,2)$，$A(6,4)$，$d_{CA}=\sqrt{(6 - 8)^2+(4 - 2)^2}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$。
也可以通过平移的性质来判断（观察图形相邻边的关系），$AD$与$EC$平行且相等，$DE$与$CA$平行且相等。
所以围成的图形是平行四边形。
故答案为：（1）$B(1,1)$，$C(8,2)$；（2）平行四边形。