《2025年同步练习册分层卷七年级数学上册人教版》

10. (3分)已知关于$x的整式ax + bx$合并后的结果为0,则下列说法正确的是(D)
[A] $a = b = 0$ 
[B] $a = b = x = 0$
[C] $a - b = 0$ 
[D] $a + b = 0$

答案： D

11. (3分)若$3x^{m + 5}y^{2}与x^{3}y^{n}$的和是单项式,则$m + n = 0$.

答案： 0

12. (3分)当$a = \frac{1}{3}$时,多项式$5a^{2} - 5a + 4 - 3a^{2} + 6a - 5$的值是$-\frac {4}{9}$.

答案： $-\frac {4}{9}$ 解析:$5a^{2}-5a+4-3a^{2}+6a-5=2a^{2}$$+a-1$，当$a=\frac {1}{3}$时，原式$=2×(\frac {1}{3})^{2}+\frac {1}{3}-$$1=\frac {2}{9}+\frac {1}{3}-1=-\frac {4}{9}.$

13. (3分)若关于$x,y的多项式2x^{2} + mx + 5y - 2nx^{2} - y + 5x + 7的值与x$的取值无关,则$m + n = -4$.

答案： -4

14. (6分)已知$-2a^{x}b^{3}与\frac{1}{3}a^{2}b^{y}$是同类项,求多项式$\frac{1}{2}x^{3} - \frac{1}{6}xy^{2} + \frac{1}{3}y^{3}$的值.

答案： 解:根据同类项的定义，得$x=2$，$y=3$.所以当$x=2$，$y=3$时，原式$=\frac {1}{2}×2^{3}-\frac {1}{6}×2×3^{2}+\frac {1}{3}×3^{3}$$=4-3+9$$=10.$

15. (6分)先化简,再求值:
(1)$2x^{3} + 3x^{2}y - xy^{2} - 3x^{2}y + xy^{2} + y^{3}$,其中$x = 1,y = -2$;
(2)$0.2x^{2}y - 0.5xy^{2} - 0.3x^{2}y + 0.7x^{2}y$,其中$x = -1,y = \frac{2}{3}$.

答案： 解:
(1)$2x^{3}+3x^{2}y-xy^{2}-3x^{2}y+xy^{2}+y^{3}$$=(3x^{2}y-3x^{2}y)+(-xy^{2}+xy^{2})+2x^{3}+y^{3}$$=0+0+2x^{3}+y^{3}$$=2x^{3}+y^{3}.$当$x=1$，$y=-2$时，原式$=2×1^{3}+(-2)^{3}=$$2-8=-6.$
(2)$0.2x^{2}y-0.5xy^{2}-0.3x^{2}y+0.7x^{2}y$$=(0.2x^{2}y-0.3x^{2}y+0.7x^{2}y)-0.5xy^{2}$$=0.6x^{2}y-0.5xy^{2}.$当$x=-1$，$y=\frac {2}{3}$时，原式$=0.6×(-1)^{2}×\frac {2}{3}-0.5×(-1)×(\frac {2}{3})^{2}$$=\frac {2}{5}+\frac {2}{9}$$=\frac {28}{45}.$

16. (6分)如图,求阴影部分的面积.

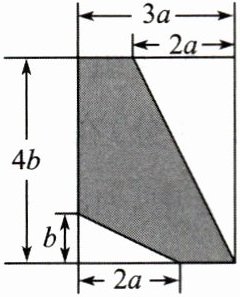
答案： 解:$3a\cdot 4b-\frac {1}{2}×2a\cdot 4b-\frac {1}{2}×2a\cdot b$$=12ab-4ab-ab=7ab$，所以阴影部分的面积为$7ab$.