第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1.(3分)$a$,$b$分别表示长方形的长和宽,则长方形的周长$l = \underline{\hspace{50pt}
2(a+b)
}$,面积$S = \underline{\hspace{50pt}ab
}$.当$a = 2\mathrm{cm}$,$b = 3\mathrm{cm}$时,$l = \underline{\hspace{50pt}10
}\mathrm{cm}$,$S = \underline{\hspace{50pt}6
}\mathrm{cm}^2$.
答案:
2(a+b) ab 10 6
2.(3分)如图,在长方形$ABCD$中,分别以$A$,$C$为圆心、$AB$的长为半径画四分之一圆,若$AB = 3$,$AD = 8$,则图中阴影部分的面积为
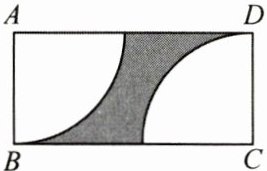
24-$\frac{9}{2}$π
.(结果保留$\pi$)
答案:
24-$\frac{9}{2}$π 解析:设AB=a,AD=b,则图中阴影部分的面积为ab-$\frac{\pi a^2}{2}$.当a=3,b=8时,图中阴影部分的面积为3×8-$\frac{9\pi}{2}$=24-$\frac{9\pi}{2}$.故答案为24-$\frac{9}{2}$π.
3.(3分)按如图所示的运算程序,能使输出的结果为3的是 (
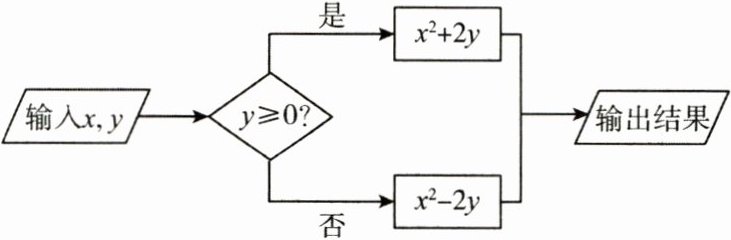

[A]$x = 1$,$y = 2$
[B]$x = -2$,$y = -2$
[C]$x = 3$,$y = 1$
[D]$x = -1$,$y = -1$
D
)

[A]$x = 1$,$y = 2$
[B]$x = -2$,$y = -2$
[C]$x = 3$,$y = 1$
[D]$x = -1$,$y = -1$
答案:
D
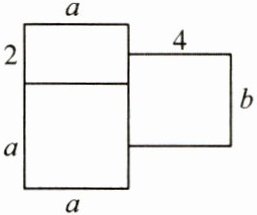
4.(10分)吕阿姨买了一套新房,她准备将地面全铺上地板砖,这套新房的平面图如图所示(单位:$\mathrm{m}$),请解答下列问题:
(1)用含$a$,$b$的代数式表示这套新房的面积;
(2)若每铺$1\mathrm{m}^2$地板砖的费用为90元,当$a = 5$,$b = 6$时,求这套新房铺地板砖所需的总费用.
(1)用含$a$,$b$的代数式表示这套新房的面积;
(2)若每铺$1\mathrm{m}^2$地板砖的费用为90元,当$a = 5$,$b = 6$时,求这套新房铺地板砖所需的总费用.

答案:
解:
(1)这套新房的面积为($a^2$+2a+4b)$m^2$.
(2)当a=5,b=6时,$a^2$+2a+4b=$5^2$+2×5+4×6=25+10+24=59($m^2$).所以这套新房铺地板砖所需的总费用为59×90=5 310(元).
(1)这套新房的面积为($a^2$+2a+4b)$m^2$.
(2)当a=5,b=6时,$a^2$+2a+4b=$5^2$+2×5+4×6=25+10+24=59($m^2$).所以这套新房铺地板砖所需的总费用为59×90=5 310(元).
5.(3分)已知$a^2 - 2a = 1$,则$3a^2 - 6a - 4$的值为 (
1 9 8 7 6 5 4 3 2 1 0 +0.5
[A]$-1$
[B]$1$
[C]$-2$
[D]$2$
A
)1 9 8 7 6 5 4 3 2 1 0 +0.5
[A]$-1$
[B]$1$
[C]$-2$
[D]$2$
答案:
A
6.(12分)如图,两叠规格相同的杯子整齐地叠放在桌面上.
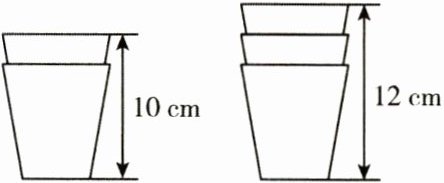
(1)按如图所示叠放时,相邻两个杯子杯口之间的高度相差
(2)若$x$个杯子按如图所示方式整齐叠放在桌面上.
①求这些杯子的顶部距离桌面的高度;(用含$x$的代数式表示)
②当$x = 12$时,求这些杯子的顶部距离桌面的高度.

1 9 8 7 6 5 4 3 2 1 0 +0.5

(1)按如图所示叠放时,相邻两个杯子杯口之间的高度相差
2
$\mathrm{cm}$.(2)若$x$个杯子按如图所示方式整齐叠放在桌面上.
①求这些杯子的顶部距离桌面的高度;(用含$x$的代数式表示)
②当$x = 12$时,求这些杯子的顶部距离桌面的高度.

1 9 8 7 6 5 4 3 2 1 0 +0.5
①由(1)得,相邻两个杯子杯口之间的高度差为2 cm,所以一个杯子的高度为10-2=8(cm),所以x个杯子按如图所示方式整齐叠放在桌面上,这些杯子的顶部距离桌面的高度是8+2(x-1)=(2x+6)cm. ②当x=12时,这些杯子的顶部距离桌面的高度是2×12+6=30(cm).
答案:
解:
(1)2
(2)①由
(1)得,相邻两个杯子杯口之间的高度差为2 cm,所以一个杯子的高度为10-2=8(cm),所以x个杯子按如图所示方式整齐叠放在桌面上,这些杯子的顶部距离桌面的高度是8+2(x-1)=(2x+6)cm. ②当x=12时,这些杯子的顶部距离桌面的高度是2×12+6=30(cm).
(1)2
(2)①由
(1)得,相邻两个杯子杯口之间的高度差为2 cm,所以一个杯子的高度为10-2=8(cm),所以x个杯子按如图所示方式整齐叠放在桌面上,这些杯子的顶部距离桌面的高度是8+2(x-1)=(2x+6)cm. ②当x=12时,这些杯子的顶部距离桌面的高度是2×12+6=30(cm).
查看更多完整答案,请扫码查看


