《2025年同步练习册分层卷七年级数学上册人教版》

11. (3分)下列等式正确的是 (B)
[A] $-2^{4}= (-2)+(-2)+(-2)+(-2)$
[B] $3^{4}= 3× 3× 3× 3$
[C] $-3^{3}= (-3)× (-3)× (-3)$
[D] $3^{4}= 4× 4× 4$

答案： B

12. (3分)在人工智能领域,二进制可以实现更强大的智能计算.现用二进制记数法来表示正整数,例如,$3= 2+1= 1× 2^{1}+1$,记作$3= (11)_{2}$；$12= 8+4= 1× 2^{3}+1× 2^{2}+0× 2^{1}+0$,记作$12= (1100)_{2}$,则$(1 010 011)_{2}$表示的正整数为 (83)
[A] 51
[B] 82
[C] 83
 [D] 156

答案： C 解析:原式$=1×2^{6}+0×2^{5}+1×2^{4}+0×2^{3}+0×2^{2}+1×2^{1}+1$$=64+0+16+0+0+2+1$$=83.$

13. (3分)《孙子算经》中记载了一段话,其大意为:今天出门看见9座堤坝,每座堤坝上有9棵树,每棵树上有9根树枝,每根树枝上有9个鸟巢,则文中的鸟巢共有 (C)
[A] $9^{3}$个
[B] $10^{3}$个
[C] $9^{4}$个
[D] $10^{4}$个

答案： C

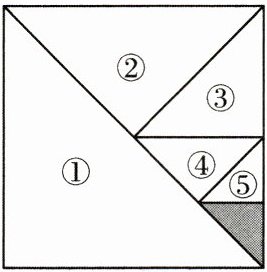
14. (3分)利用如图所示的图形,可求$\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\frac{1}{2^{4}}+\frac{1}{2^{5}}$的值是 (C)

 
 
[A] $\frac{27}{32}$
[B] $\frac{29}{32}$
[C] $\frac{31}{32}$
[D] $\frac{33}{32}$

答案： C 解析:假设面积为1，则$\frac {1}{2}+\frac {1}{2^{2}}+\frac {1}{2^{3}}+\frac {1}{2^{4}}+\frac {1}{2^{5}}$即为①+②+③+④+⑤的面积，题图中阴影部分的面积为$\frac {1}{2^{5}},$所以①+②+③+④+⑤的面积为$1-\frac {1}{2^{5}}=\frac {31}{32}.$所以$\frac {1}{2}+\frac {1}{2^{2}}+\frac {1}{2^{3}}+\frac {1}{2^{4}}+\frac {1}{2^{5}}$的值为$\frac {31}{32}.$

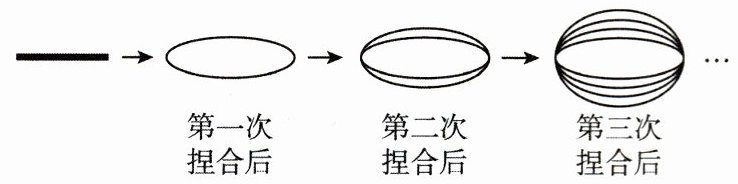
15. (3分)拉面馆的师傅用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如图所示.这样捏合到第8次后可拉出256根面条.

答案： 8

16. (15分)阅读材料:求$1+2+2^{2}+2^{3}+… +2^{2023}+2^{2024}$的值.
解:设$S= 1+2+2^{2}+2^{3}+… +2^{2023}+2^{2024}$.①
将等式①的两边同乘2,
得$2S= 2+2^{2}+2^{3}+2^{4}+… +2^{2024}+2^{2025}$.②
②-①,得$2S - S = 2^{2025} - 1$,
即$S = 2^{2025} - 1$.
所以$1+2+2^{2}+2^{3}+… +2^{2023}+2^{2024}= 2^{2025}-1$.
请仿照此法计算:
(1) 填空: $1+3+3^{2}+3^{3}+3^{4}+3^{5}=$$\frac {3^{6}-1}{2}$；
(2) 求$1+7+7^{2}+7^{3}+… +7^{2025}+7^{2026}$的值.
设$S=1+7+7^{2}+7^{3}+... +7^{2025}+7^{2026}$.①将等式两边同时乘7，得$7S=7+7^{2}+7^{3}+7^{4}+... +7^{2026}+7^{2027}$.②②-①，得$7S-S=7^{2027}-1,$即$S=\frac {7^{2027}-1}{6}.$所以$1+7+7^{2}+7^{3}+... +7^{2025}+7^{2026}=\frac {7^{2027}-1}{6}.$

答案：
(1)$\frac {3^{6}-1}{2}$；
(2)设$S=1+7+7^{2}+7^{3}+... +7^{2025}+7^{2026}$.①将等式两边同时乘7，得$7S=7+7^{2}+7^{3}+7^{4}+... +7^{2026}+7^{2027}$.②②-①，得$7S-S=7^{2027}-1,$即$S=\frac {7^{2027}-1}{6}.$所以$1+7+7^{2}+7^{3}+... +7^{2025}+7^{2026}=\frac {7^{2027}-1}{6}.$