《2025年同步练习册分层卷七年级数学上册人教版》

10. (3分)请写出一个比$-4\frac{2}{3}$大的负整数为-4(答案不唯一).(写出一个即可)

答案： -4(答案不唯一)

11. (3分)比较大小:$-\frac{2023}{2024}$＞$-\frac{2024}{2025}$.(填 “$＞$”“$＜$”或“$=$”)

答案： ＞ 解析：$1+\left(-\dfrac{2023}{2024}\right)=\dfrac{1}{2024}$，$1+\left(-\dfrac{2024}{2025}\right)=\dfrac{1}{2025}$。
因为$\dfrac{1}{2024}$，$\dfrac{1}{2025}$分子相同，分母不同，且2024＜2025，
所以$\dfrac{1}{2024}＞\dfrac{1}{2025}$。所以$-\dfrac{2023}{2024}＞-\dfrac{2024}{2025}$。

12. (3分)对于有理数$a,b$,若$a\gt -2,b\gt a$,则$b$＞$-2$.(填“$＞$”“$＜$”或“$=$”)

答案： ＞

13. (3分)如图,四个有理数在数轴上的对应点分别为点$M,P,N,Q$.若点$M,N$表示的有理数互为相反数,则图中表示绝对值最大的数所对应的点是点Q.

答案： 点Q 解析：因为点M，N表示的有理数互为相反数，
所以原点在M，N的中点处，
所以原点的位置大约在点O(如图)。
所以绝对值最大的数所对应的点是点Q。
　　　　　N Q O P

14. (8分)(1)把下列各数:$-5,3\frac{1}{2},0,-\frac{5}{2},|-4|$在数轴上表示出来;
(2)将上列各数用“$＜$”按从小到大的顺序连接.

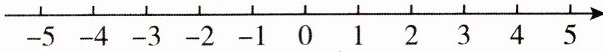
答案：
解：
(1)如图。
　　　
(2)由
(1)可知$-5＜-\dfrac{5}{2}＜0＜3\dfrac{1}{2}＜|-4|$。

15. (13分)有理数$a,b,c$在数轴上对应点的位置如图所示.
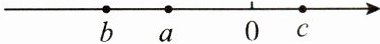
(1)用“$＞$”“$＜$”或“$=$”填空:$a$＜$0,b$＜$0,c$＞$0$.
(2)利用数轴化简:
①$|a|=$$-a$;②$|b|=$$-b$;③$|c|=$$c$;④$|-a|=$$-a$;⑤$|-b|=$$-b$;⑥$|-c|=$$c$.
(3)试将$a,b,c,-a,-b,-c,0$用“$＜$”连接起来.

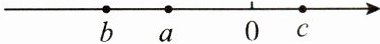
$b＜a＜-c＜0＜c＜-a＜-b$

答案： 解：
(1)由所给数轴可知，a＜0，b＜0，c＞0。
故答案为＜；＜；＞。
(2)①$-a$ ②$-b$ ③$c$ ④$-a$ ⑤$-b$ ⑥$c$
(3)将a，b，c，$-a$，$-b$，$-c$，0在数轴上表示出来如图所示。
　　　　　b a -c 0 c -a -b
所以$b＜a＜-c＜0＜c＜-a＜-b$。