《2025年配套练习与检测四年级数学上册北师大版》

4. (1)需要多少个箱子？用竖式算一算,并说一说你的计算过程。

(2)如果每箱能装52个球,这些球能装多少箱？还剩几个？说一说试商和计算过程。

答案： 1. （1）
已知有$256$个球，每箱装$32$个，求箱子数，即$256÷32$。
用竖式计算：
先看被除数的前两位$25$，$25\lt32$，再看被除数的前三位$256$。
想$32×8 = 256$，所以$256÷32 = 8$。
计算过程：$32×8 = 256$，刚好整除，所以需要$8$个箱子。
2. （2）
已知有$256$个球，每箱装$52$个，求能装的箱数和剩余球数，即$256÷52$。
试商过程：
把$52$看作$50$来试商，因为$50×5 = 250$，接近$256$。
计算过程：
$52×4 = 208$，$256−208 = 48$；$52×5 = 260\gt256$。
所以$256÷52 = 4\cdots\cdots48$。
综上，（1）需要$8$个箱子；（2）能装$4$箱，还剩$48$个。

5. 组装下面这样一个架子需要层板4块、立柱12根、三角片16个、防滑垫4个、螺丝48个。张师傅现在有82块层板、227根立柱、250个三角片、50个防滑垫和550个螺丝。他最多可以组装几个这样的架子？

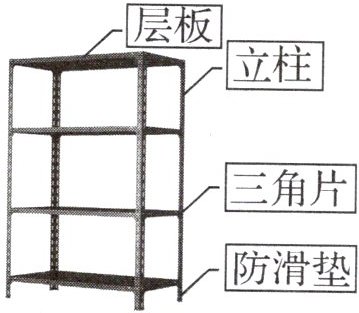
答案： 82÷4=20(个)……2(块)
227÷12=18(个)……11(根)
250÷16=15(个)……10(个)
50÷4=12(个)……2(个)
550÷48=11(个)……22(个)
最多可以组装11个