《2025年作业本江西教育出版社六年级数学上册人教版》

1. 看图列式计算。

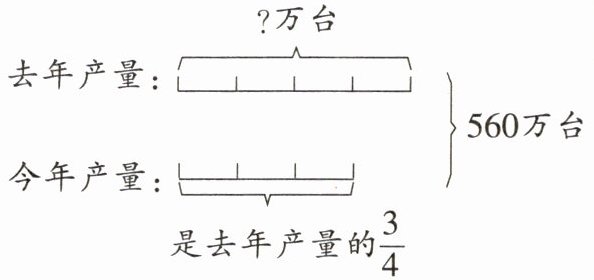
答案： 此题为计算题，无选项。

2. 蜜蜂和苍蝇每秒共振动翅膀500次,蜜蜂每秒振动翅膀的次数是苍蝇的$\frac{3}{2}$,蜜蜂和苍蝇每秒各振动翅膀多少次?

答案： 蜜蜂每秒振动翅膀300次，苍蝇每秒振动翅膀200次。

3. 标准的篮球场是一个长方形,它的周长是86m,宽是长的$\frac{15}{28}$。标准篮球场的长、宽分别是多少?

答案： 设标准篮球场的长是$x$米，因为宽是长的$\frac{15}{28}$，所以宽是$\frac{15}{28}x$米。
长方形周长公式：$周长 = 2×(长 + 宽)$，已知周长是$86$米，可列方程：
$2×(x + \frac{15}{28}x) = 86$
$2×(\frac{28}{28}x + \frac{15}{28}x) = 86$
$2×\frac{43}{28}x = 86$
$\frac{43}{14}x = 86$
$x = 86×\frac{14}{43}$
$x = 28$
宽：$\frac{15}{28}×28 = 15$（米）
答：标准篮球场的长是$28$米，宽是$15$米。

4. 体育中心在举办合唱比赛。比赛结束后,如果只开A出口,全部人员离场需要10分钟;如果只开B出口,全部人员离场需要15分钟;如果只开C出口,全部人员离场需要20分钟。
(1)如果A、B两个出口同时开放,多少分钟能让全部人员离场?
(2)如果A、B、C三个出口同时开放,多少分钟能让全部人员离场?
(3)如果B、C两个出口同时开放,多少分钟能让$\frac{2}{3}$的人员离场?

答案：
(1)把全部人员看作单位“1”，A出口每分钟离场人员占比为$\frac{1}{10}$，B出口每分钟离场人员占比为$\frac{1}{15}$。
A、B同时开放每分钟离场占比：$\frac{1}{10} + \frac{1}{15} = \frac{3}{30} + \frac{2}{30} = \frac{5}{30} = \frac{1}{6}$
全部离场时间：$1÷\frac{1}{6} = 6$（分钟）
(2)A、B、C同时开放每分钟离场占比：$\frac{1}{10} + \frac{1}{15} + \frac{1}{20}$
$=\frac{6}{60} + \frac{4}{60} + \frac{3}{60} = \frac{13}{60}$
全部离场时间：$1÷\frac{13}{60} = \frac{60}{13}$（分钟）
(3)B、C同时开放每分钟离场占比：$\frac{1}{15} + \frac{1}{20} = \frac{4}{60} + \frac{3}{60} = \frac{7}{60}$
$\frac{2}{3}$人员离场时间：$\frac{2}{3}÷\frac{7}{60} = \frac{2}{3}×\frac{60}{7} = \frac{40}{7}$（分钟）
(1)6分钟
(2)$\frac{60}{13}$分钟
(3)$\frac{40}{7}$分钟

5. 明明放学后,从学校步行回家,走了全程的$\frac{2}{5}$后,他距离两地中点还有200m。明明家到学校共有多少米?

答案： 设明明家到学校共有$x$米。
中点即全程的$\frac{1}{2}$，走了全程的$\frac{2}{5}$后距离中点的距离为$\frac{1}{2}x - \frac{2}{5}x$。
$\frac{1}{2}x - \frac{2}{5}x = 200$
$\frac{5}{10}x - \frac{4}{10}x = 200$
$\frac{1}{10}x = 200$
$x = 200 ÷ \frac{1}{10}$
$x = 2000$
答：明明家到学校共有2000米。