《2025年新课程学习与测评同步学习七年级数学上册湘教版》

4. 计算：
(1) $ -(-\frac{3}{4})^3 × (-2)^4 $；
(2) $ \frac{2^3}{5} × (-\frac{5}{4})^2 $.

答案： 解：
(1)$-\left(-\dfrac{3}{4}\right)^3×(-2)^4=\dfrac{27}{64}×16=\dfrac{27}{4}$；
(2)$\dfrac{2^3}{5}×\left(-\dfrac{5}{4}\right)^2=\dfrac{8}{5}×\dfrac{25}{16}=\dfrac{5}{2}$

1. 有下列各数 $ (-3)^3 $,$ -(-3) $,$ (-3)^4 $,$ -|-3| $,$ -3^3 $.其中,负数有( ).

A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 5 $ 个

答案： B 提示：负数有$(-3)^5$,$-\vert-3\vert$,$-3^3$,共3个

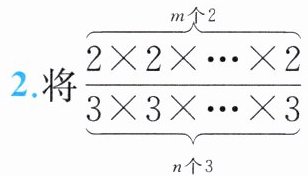
2. 将 $ \underbrace{2 × 2 × … × 2}_{m 个 2} ÷ \underbrace{3 × 3 × … × 3}_{n 个 3} $ 写成幂的形式,正确的是( ).


A.$ \frac{2^m}{3^n} $
B.$ \frac{2m}{3^n} $
C.$ \frac{2^m}{3n} $
D.$ \frac{m^2}{3n} $

答案： A

3. [数学文化]《庄子》中记载：“一尺之棰,日取其半,万世不竭.”这句话的意思是：一尺长的木棍,每天截取它的一半,永远也截不完.按此方式截一根长为 $ 1 $ 的木棍,第 $ 5 $ 天截取后,木棍剩余的长度是( ).

A.$ 1 - \frac{1}{2^5} $
B.$ 1 - \frac{1}{2^4} $
C.$ \frac{1}{2^5} $
D.$ \frac{1}{2^4} $

答案： C 提示：由题意知，第1天截取后剩余长度为$1×\left(1-\dfrac{1}{2}\right)=\dfrac{1}{2}$,第2天截取后剩余长度为$\dfrac{1}{2}×\left(1-\dfrac{1}{2}\right)=\dfrac{1}{4}=\dfrac{1}{2^2}$,第3天截取后剩余长度为$\dfrac{1}{2^2}×\left(1-\dfrac{1}{2}\right)=\dfrac{1}{2^3}$,…,第n天截取后剩余长度为$\dfrac{1}{2^n}$,所以第5天截取后剩余长度为$\dfrac{1}{2^5}$

4. $ (-3)^4 $ 表示“______”,计算结果是______；$ -3^4 $ 表示“______”,计算结果是______.

答案： $-3$的4次方 81 3的4次方的相反数 $-81$

5. 计算：
(1) $ 1.5^2 × 2^4 $；
(2) $ -(\frac{2}{3})^3 × (\frac{1}{2})^2 $；
(3) $ (-\frac{2}{5})^2 × (-2\frac{1}{2})^3 $.

答案：
(1)$1.5^2×2^4=\left(\dfrac{3}{2}\right)^2×2^4=\dfrac{9}{4}×16=36$；
(2)$-\left(\dfrac{2}{3}\right)^3×\left(\dfrac{1}{2}\right)^2=-\dfrac{8}{27}×\dfrac{1}{4}=-\dfrac{2}{27}$；
(3)$\left(-\dfrac{2}{5}\right)^2×\left(-2\dfrac{1}{2}\right)^3=\dfrac{4}{25}×\left(-\dfrac{125}{8}\right)=-\dfrac{5}{2}$