《2025年云南省标准教辅同步指导训练与检测配套测试卷六年级数学上册人教版》

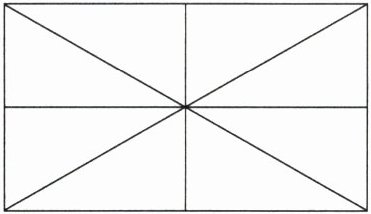
1.数一数,下图中一共有(16)个三角形。

答案： 16

2.(1)$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}=$($\frac{127}{128}$)
(2)$\frac{9}{2},\frac{16}{3},\frac{25}{4},\frac{36}{5}$,($\frac{49}{6}$),($\frac{64}{7}$)。

答案：
(1) 设$S = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128}$，则$2S = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64}$，$2S - S = 1 - \frac{1}{128}$，$S = \frac{127}{128}$
(2) 分子依次为$3^2 = 9$，$4^2 = 16$，$5^2 = 25$，$6^2 = 36$，下一个分子为$7^2 = 49$，再下一个为$8^2 = 64$；分母依次为$2$，$3$，$4$，$5$，下一个分母为$6$，再下一个为$7$，所以括号里依次为$\frac{49}{6}$，$\frac{64}{7}$
(1)$\frac{127}{128}$；
(2)$\frac{49}{6}$，$\frac{64}{7}$

3.0.72里面有(72)个1%,有(9)个8%。

答案： 解析：本题考查了百分数和小数的换算以及除法运算。
首先，我们需要将0.72转换为百分数形式，即乘以100%，得到72%。
接着，我们来看第一个空，需要找出0.72里面有多少个1%。
由于1%就是0.01，所以我们可以用0.72除以0.01来找出答案，即$0.72 ÷ 0.01=72$。
因此，0.72里面有72个1%。
然后，我们来看第二个空，需要找出0.72里面有多少个8%。
8%可以转换为小数0.08，所以我们可以用0.72除以0.08来找出答案，即$0.72 ÷ 0.08=9$。
因此，0.72里面有9个8%。
答案：72；9。

4.一个数的$\frac{2}{3}$是8,则这个数的$\frac{1}{6}$是(2)。

答案： 解析：题目考查分数运算和方程的建立与求解。需要通过已知一个数的几分之几是多少，反推出这个数，然后再求这个数的几分之几。
设这个数为$x$，根据题意可以列出方程：
$\frac{2}{3}x = 8$，
解这个方程得到：
$x = 8 ÷ \frac{2}{3} = 12$，
然后求这个数的$\frac{1}{6}$，即：
$12 × \frac{1}{6} = 2$，
答案：2。

5.某商品的现价比原价降低了$\frac{1}{8}$,则现价是原价的($\frac{7}{8}$)。

答案： 设原价为单位“1”。
现价 = 原价 - 降低的部分 = $1 - \frac{1}{8} = \frac{7}{8}$
现价是原价的$\frac{7}{8}$。
$\frac{7}{8}$

6.有三个数的平均数是6,这三个数的比是2:3:4,这三个数中最小的数是(4),最大的数是(8)。

答案： 解析：本题可先根据平均数求出三个数的总和，再根据三个数的比例关系分别求出最小数和最大数。
步骤一：求出三个数的总和
已知三个数的平均数是$6$，根据平均数的定义“平均数是指在一组数据中所有数据之和再除以这组数据的个数”，可得这三个数的总和为：$6×3 = 18$。
步骤二：求出三个数分别占总和的比例
已知这三个数的比是$2:3:4$，那么总份数为：$2 + 3 + 4 = 9$（份）。
所以这三个数分别占总和的比例为：
第一个数占总和的$\frac{2}{9}$；
第二个数占总和的$\frac{3}{9}$；
第三个数占总和的$\frac{4}{9}$。
步骤三：分别求出最小数和最大数
最小数：因为$\frac{2}{9}\lt\frac{3}{9}\lt\frac{4}{9}$，所以最小数占总和的$\frac{2}{9}$，则最小数为：$18×\frac{2}{9} = 4$。
最大数：最大数占总和的$\frac{4}{9}$，则最大数为：$18×\frac{4}{9} = 8$。
答案：4；8

7.某种细胞每30分钟就能由1个分裂成3个,经过2小时,这种细胞能由1个分裂成(81)个。

答案： 解析：本题可根据细胞分裂的规律，结合经过的时间与分裂周期的关系来计算细胞的数量。
步骤一：计算$2$小时内细胞分裂的次数
已知细胞每$30$分钟分裂一次，$2$小时换算成分钟为$2×60 = 120$分钟。
则$2$小时内细胞分裂的次数为$120÷30 = 4$次。
步骤二：分析细胞分裂的规律并计算最终细胞数量
因为$1$个细胞每$30$分钟分裂成$3$个，即每次分裂后细胞数量变为原来的$3$倍。
经过$1$次分裂后，细胞数量为$1×3 = 3$个；
经过$2$次分裂后，细胞数量为$3×3 = 3^2 = 9$个；
经过$3$次分裂后，细胞数量为$9×3 = 3^3 = 27$个；
以此类推，经过$n$次分裂后，细胞数量为$3^n$个。
现在经过$4$次分裂，所以细胞数量为$3^4 = 81$个。
答案：$81$

8.一个分数的分子与分母的和是13,差是5,这个分数是($\frac{4}{9}$)。

答案： 解析：
这是一个关于分数的问题，同时涉及到分子和分母的和与差。需要找到满足条件的分子和分母。
设这个分数的分子为$x$，分母为$y$。
根据题目，可以建立以下方程：
分子与分母的和是13，所以 $x + y = 13$。
分子与分母的差是5，所以 $x - y = 5$ 或 $y - x = 5$（考虑到可能是分子小于分母）。
现在来解这组方程。
首先，考虑 $x - y = 5$ 的情况：
$\{\begin{array}{l}x + y = 13 \\ x - y = 5\end{array}$
解这个方程组，得到：
$\{\begin{array}{l}x = 9 \\ y = 4\end{array}$
但这个解不合适，因为分母通常大于分子（除非特别说明，如带分数或假分数）。
接着，考虑 $y - x = 5$ 的情况：
$\{\begin{array}{l}x + y = 13 \\ y - x = 5\end{array}$
解这个方程组，得到：
$\{\begin{array}{l}x = 4 \\ y = 9\end{array}$
这个解是合理的，因为分子小于分母。
所以，这个分数是 $\frac{4}{9}$。
答案：
这个分数是 $\frac{4}{9}$。

9.一辆小汽车行驶6km耗油$\frac{3}{5}$kg,照这样计算,这辆小汽车行驶1km要耗油($\frac{1}{10}$)kg,平均每千克油可供这辆小汽车行驶(10)km。

答案： 解析：
本题考查分数除法的应用。
根据题意，一辆小汽车行驶6km耗油$\frac{3}{5}kg$。
要计算这辆小汽车行驶1km要耗油多少kg，需要将总耗油量除以总行驶距离，即：
$\frac{3}{5} ÷ 6 = \frac{3}{5} × \frac{1}{6} = \frac{1}{10}(kg)$；
接下来，计算平均每千克油可供这辆小汽车行驶多少km。
需要将总行驶距离除以总耗油量，即：
$6 ÷ \frac{3}{5} = 6 × \frac{5}{3} = 10(km)$。
答案：
这辆小汽车行驶1km要耗油( $\frac{1}{10}$)kg；
平均每千克油可供这辆小汽车行驶( 10 )km。

10.小明面向西偏北45°的方向站好,当他向右转90°后,他面向的方向是(东偏北45°)。

答案： 小明初始面向西偏北45°，向右转90°即按顺时针方向旋转90°。西偏北45°顺时针旋转90°后，方向为东偏北45°。
东偏北45°