《2025年新编基础训练七年级数学上册通用版S》

1. $-\dfrac{1}{5}$的相反数是(C)
A.$-5$
B.$-\dfrac{1}{5}$
C.$\dfrac{1}{5}$
D.$5$

答案： C

2. 如图,不完整的数轴(单位长度为1)上有三个点$A$,$B$,$C$,若点$A$,$B$表示的数互为相反数,则点$C$对应的数是(C)


A.$-2$
B.$0$
C.$1$
D.$4$

答案： C

3. 向指定方向变化用正数表示,向指定方向的相反方向变化用负数表示. “体重减少$1.5$kg”换一种说法可以叙述为“体重增加-1.5kg”.

答案： -1.5

4. 若$a$是最小的自然数,$b$是最大负整数的相反数,$c$是绝对值最小的有理数,则$a^{2} + b + c$的值为1.

答案： 1

5. 当$x = $2024时,$2025 - |2024 - x|$取得最大值,且最大值为2025.

答案： 2024 2025

6. (2025·北京)如图,观察数轴,解答下列问题：
(1)$A$点表示的有理数是____,表示有理数$\dfrac{5}{2}$的点是____；
(2)在数轴上,用点$M$,$N分别表示有理数-\dfrac{3}{2}$和6；
(3)用“$＜$”将点$A$,$B$,$O$,$M$,$N$表示的数连接起来.

答案：
解:
(1)-5 点 B
(2)如图所示.
(3)$-5＜-\frac{3}{2}＜0＜\frac{5}{2}＜6$.

7. (2024·合肥)在$-\dfrac{1}{2024}$,$-1$,$0$,$\dfrac{1}{2024}$四个数中,最大的数是(D)
A.$-\dfrac{1}{2024}$
B.$-1$
C.$0$
D.$\dfrac{1}{2024}$

答案： D

8. 计算：(1)$125 × 3.67 × 6 × 8 ×\left(-\dfrac{1}{6}\right)$；
(2)$(-24) × 0.125 + 24 × \dfrac{3}{8} + (-24) × \dfrac{1}{4}$；
(3)$(-1)^{3} - 1\dfrac{1}{4} × \dfrac{4}{9} ÷ [1 + 2 × (-3)]$.

答案： 解:
(1)原式$=125×8×[6×(-\frac{1}{6})]×3.67=1000×(-1)×3.67=-3670$.
(2)原式$=24×(-\frac{1}{8})+24×\frac{3}{8}-24×\frac{1}{4}=24×(-\frac{1}{8}+\frac{3}{8}-\frac{1}{4})=24×0=0$.
(3)原式$=-1+\frac{5}{4}×\frac{4}{9}×\frac{1}{5}=-1+\frac{1}{9}=-\frac{8}{9}$.

9. 某中学积极倡导阳光体育运动,开展了排球垫球比赛. 下表为七年级某班45人参加排球垫球比赛的情况,标准为每人垫球25个.

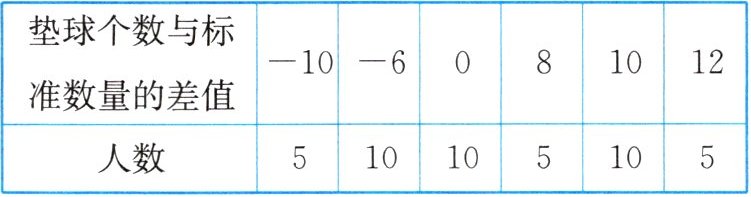
(1)这个班45人平均每人垫球多少个？
(2)规定垫球达到标准数量记0分,超过标准数量,每多垫1个加2分；未达到标准数量,每少垫1个扣1分,则这个班的垫球总共获得多少分？

答案： 解:
(1)$-10×5+(-6)×10+0×10+8×5+10×10+12×5=-50-60+0+40+100+60=90$(个),$(25×45+90)÷45=1215÷45=27$(个).答:这个班45人平均每人垫球27个.
(2)$2×(8×5+10×10+12×5)-1×(| -10 |×5+| -6 |×10)=290$(分).答:这个班的垫球总共获得290分.