第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
【例题】阅读材料:
你知道二维码吗?它是一种编码,通过表示1和0的黑白小方块排列成图案来传递信息.二维码广泛应用于我们的生活.
你知道二维码究竟是怎样生成的吗?你想亲自制作一个二维码吗?首先来了解一个定义:定义符号“⊕”表示一种运算,叫作“异或”运算,即当$a = b$时,$a\oplus b = 0$;当$a\neq b$时,$a\oplus b = 1$.
下面就让我们试着为“BHSF”制作一个二维码吧!
步骤一:
查表可得字母“B”的二进制编码为01000010,“H”为01001000,“S”为01010011,“F”为01000110.
步骤二:
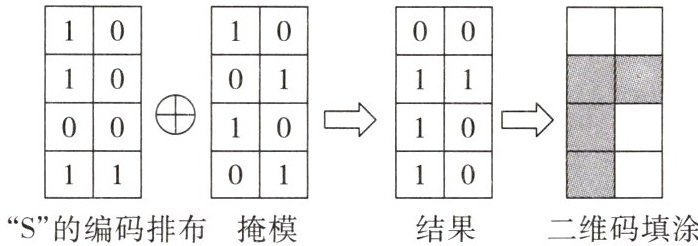
将每个字母的编码按照一定的顺序排布在方格内,例如字母“S”的编码排布如图第一个表格.然后将编码排布与事先排布好0和1的表格(称为掩模)进行“方格一一对应”的“异或”运算(如图第三个表格),并将结果中1的位置填涂灰色,0的位置填涂白色(如图第四个表格).
解决问题:
(1)请根据上面的定义将表格补充完整;

(2)仿照上面的步骤二,完成“F”的编码排布、运算及二维码填涂.
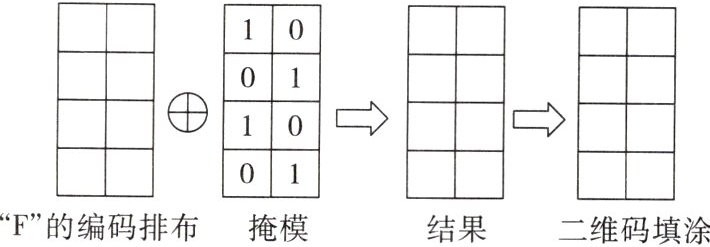
你知道二维码吗?它是一种编码,通过表示1和0的黑白小方块排列成图案来传递信息.二维码广泛应用于我们的生活.
你知道二维码究竟是怎样生成的吗?你想亲自制作一个二维码吗?首先来了解一个定义:定义符号“⊕”表示一种运算,叫作“异或”运算,即当$a = b$时,$a\oplus b = 0$;当$a\neq b$时,$a\oplus b = 1$.
下面就让我们试着为“BHSF”制作一个二维码吧!
步骤一:
查表可得字母“B”的二进制编码为01000010,“H”为01001000,“S”为01010011,“F”为01000110.
步骤二:
将每个字母的编码按照一定的顺序排布在方格内,例如字母“S”的编码排布如图第一个表格.然后将编码排布与事先排布好0和1的表格(称为掩模)进行“方格一一对应”的“异或”运算(如图第三个表格),并将结果中1的位置填涂灰色,0的位置填涂白色(如图第四个表格).

解决问题:
(1)请根据上面的定义将表格补充完整;

(2)仿照上面的步骤二,完成“F”的编码排布、运算及二维码填涂.

答案:
(1)根据“异或”运算的定义填写表格如下:
a b 结果
0 0 0
1 0 1
0 1 1
1 1 0
(2)“F”的编码排布、运算及二维码填涂如下:

(1)根据“异或”运算的定义填写表格如下:
a b 结果
0 0 0
1 0 1
0 1 1
1 1 0
(2)“F”的编码排布、运算及二维码填涂如下:

(1)某种二维码尺寸为$25×25$,共有625个小方块,除去用于定位、纠错等功能的方块之外,最终剩下478个小方块,总共可以组合成多少种不同的二维码?
答案:
(1)$2^{478}$.
(1)$2^{478}$.
(2)据不完全统计,每天二维码的全球使用量高达100多亿,一年使用36500亿个,那么使用完题(1)中计算得到的二维码需要多少年?有人担心二维码会被用完,你认为二维码会被用完吗?用计算器计算并说明你的观点.(提示:宇宙诞生至今约138亿年,即$1.38×10^{10}$年)
答案:
(2)36500亿$=3.65×10^{12}$,
$1.38×10^{10}×3.65×10^{12}=5.037×10^{22}$,
而$5.037×10^{22}$远远小于$2^{478}$,
所以从理论上讲,二维码的数量有限,会被用完,但是与宇宙诞生至今的时间相比较,二维码不会被用完.
(2)36500亿$=3.65×10^{12}$,
$1.38×10^{10}×3.65×10^{12}=5.037×10^{22}$,
而$5.037×10^{22}$远远小于$2^{478}$,
所以从理论上讲,二维码的数量有限,会被用完,但是与宇宙诞生至今的时间相比较,二维码不会被用完.
查看更多完整答案,请扫码查看


