第130页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
3. 甲、乙两人分别从相距20km的A,B两地出发,相向而行.如图所示的是小华绘制的甲、乙两人运动两次的情形.设甲的速度是x km/h,乙的速度是y km/h.根据题意,可列出的方程组是

{2.5x+2y=20,x+y+11=20}
.
答案:
{2.5x+2y=20,x+y+11=20}
4. 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了
9
场.
答案:
9
5. 在一次足球选拔赛中,有12支球队参加选拔,每一队都要与另外的球队比赛一场,计分规则为胜一场计3分,平一场计1分,负一场计0分.比赛结束时,某球队所胜场数是所负场数的2倍,共得20分,则这支球队胜、负各几场?
答案:
解:设这支球队负x场,
则胜2x场,平y场.
根据题意,得{2x×3+y=20,2x+x+y=11},解得{x=3,y=2}.
所以2x=6.
答:这支球队胜6场,负3场.
则胜2x场,平y场.
根据题意,得{2x×3+y=20,2x+x+y=11},解得{x=3,y=2}.
所以2x=6.
答:这支球队胜6场,负3场.
6. 小明、小亮、小颖玩飞镖游戏,他们每人投靶5次,中靶情况如图所示.规定投中同一圆环得分相同,若小明得分21分,小亮得分17分,则小颖得分为(
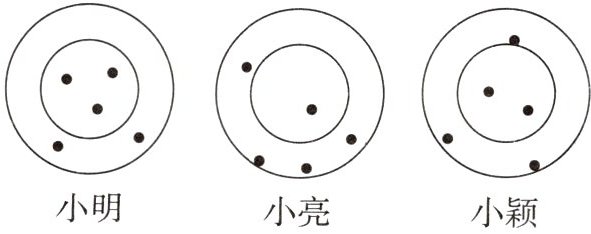
A.19分
B.20分
C.21分
D.22分
A
)
A.19分
B.20分
C.21分
D.22分
答案:
A
7. 我国古代数学问题:以绳测井,将绳三折测之,绳多四尺;将绳四折测之,绳多一尺.井深几何?这段话的意思是用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.井深几尺?该问题中的井深是
8
尺.
答案:
8
8. (2025·亳州)甲、乙两地相距200km,一列慢车从甲地开出,一列快车从乙地开出.如果两车同向而行,那么快车10h后追上慢车;如果两车相向而行,那么2h后两车相遇,试问:
(1)两车的速度分别是多少?
(2)若两车同时相向而行,多少时间可以相距100km?(要求:画出线段示意图表示数量关系)
(1)两车的速度分别是多少?
(2)若两车同时相向而行,多少时间可以相距100km?(要求:画出线段示意图表示数量关系)
答案:
解:
(1)设快车、慢车的速度分别为xkm/h,ykm/h,且x>y.
由题意,得{10x-10y=200,2x+2y=200},解得{x=60,y=40}.
答:快车、慢车的速度分别为60km/h,40km/h.
(2)设时间为th时,两车相距100km.
①两车未相遇前相距100km,

则(60+40)t+100=200,解得t=1;
②两车相遇后相距100km,

则(60+40)t−100=200,解得t=3.
答:两车同时相向而行,1h或3h可以相距100km.
解:
(1)设快车、慢车的速度分别为xkm/h,ykm/h,且x>y.
由题意,得{10x-10y=200,2x+2y=200},解得{x=60,y=40}.
答:快车、慢车的速度分别为60km/h,40km/h.
(2)设时间为th时,两车相距100km.
①两车未相遇前相距100km,

则(60+40)t+100=200,解得t=1;
②两车相遇后相距100km,

则(60+40)t−100=200,解得t=3.
答:两车同时相向而行,1h或3h可以相距100km.
9. 一艘轮船在相距90km的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6h,逆流航行比顺流航行多用4h.
(1)求该轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间建造丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,则甲、丙两地相距多少千米?
(1)求该轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间建造丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,则甲、丙两地相距多少千米?
答案:
解:
(1)设该轮船在静水中的速度是xkm/h,水流速度是ykm/h.
依题意,得{6(x+y)=90,(6+4)(x-y)=90},解得{x=12,y=3}.
答:该轮船在静水中的速度是12km/h,水流速度是3km/h.
(2)设甲、丙两地相距akm,
则乙、丙两地相距(90−a)km.
依题意,得$\frac{a}{12+3}$=$\frac{90−a}{12−3}$,解得a=$\frac{225}{4}$.
答:甲、丙两地相距$\frac{225}{4}$km.
(1)设该轮船在静水中的速度是xkm/h,水流速度是ykm/h.
依题意,得{6(x+y)=90,(6+4)(x-y)=90},解得{x=12,y=3}.
答:该轮船在静水中的速度是12km/h,水流速度是3km/h.
(2)设甲、丙两地相距akm,
则乙、丙两地相距(90−a)km.
依题意,得$\frac{a}{12+3}$=$\frac{90−a}{12−3}$,解得a=$\frac{225}{4}$.
答:甲、丙两地相距$\frac{225}{4}$km.
查看更多完整答案,请扫码查看


