《2025年配套综合练习甘肃七年级数学上册北师大版》

7. 观察下列等式：$1×\frac{1}{2} = 1 - \frac{1}{2}$,$2×\frac{2}{3} = 2 - \frac{2}{3}$,$3×\frac{3}{4} = 3 - \frac{3}{4}$,…,解答下列问题：
(1) 请写出第 9 个等式；
(2) 猜想第$n$个等式。

答案： 解:
(1)$9×\frac{9}{10}=9-\frac{9}{10}$。
(2)猜想:$n×\frac{n}{n+1}=n-\frac{n}{n+1}$。

8. 【综合与实践】阶梯的每个台阶上都标着一个数,从下到上的第 1 个至第 4 个台阶上依次标着$-5$,$-2$,1,9,且任意相邻四个台阶上数的和都相等。
尝试：
(1) 求前 4 个台阶上的数的和；
(2) 求第 5 个台阶上的数。
应用：
(3) 求从下到上前 31 个台阶上的数的和。
发现：
(4) 试用含$k$($k$为正整数)的式子表示出数“1”所在台阶数。

答案： 解:
(1)$-5-2+1+9=3$。
(2)设第5个台阶上的数为x。由题意,得$-2+1+9+x=3$,解得$x=-5$。
(3)每4个相邻台阶上的数的和为3,前31个台阶上的数的和为$7×3+(-5-2+1)=15$。
(4)发现“1”出现在每组4个数的第3个,也就是第3、第7、第11……个台阶上,且$3=4×1-1$,$7=4×2-1$,$11=4×3-1$,…,所以“1”出现的台阶数为$4k-1$。

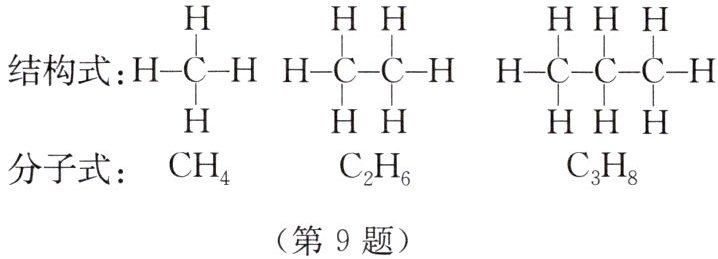
9. 【跨学科】观察下面三种化合物的结构式及分子式,如果按其规律,那么下一种化合物的分子式应该是$C_{4}H_{10}$。

答案： $C_{4}H_{10}$