第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
12. 【数学文化】希腊著名的毕达哥拉斯学派把 $1,3,6,10,…$ 这样的数称为“三角形数”,而把 $1,4,9,16,…$ 这样的数称为“正方形数”。从中可以发现,任何一个大于 $1$ 的“正方形数”都可以看作两个相邻“三角形数”之和。下列等式中,符合这一规律的是(
A.$13 = 3 + 10$
B.$25 = 9 + 16$
C.$36 = 15 + 21$
D.$49 = 18 + 31$
C
)。A.$13 = 3 + 10$
B.$25 = 9 + 16$
C.$36 = 15 + 21$
D.$49 = 18 + 31$
答案:
C
1. 如图,依此规律堆放圆木,第 10 堆需要圆木(
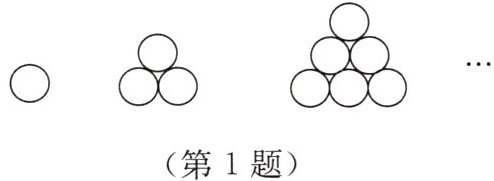
A.50 根
B.55 根
C.60 根
D.65 根
]
B
)。
A.50 根
B.55 根
C.60 根
D.65 根
]
答案:
B
2. 1766 年德国人提丢斯发现,太阳系中的行星到太阳的距离遵循一定的规律,如下表所示:
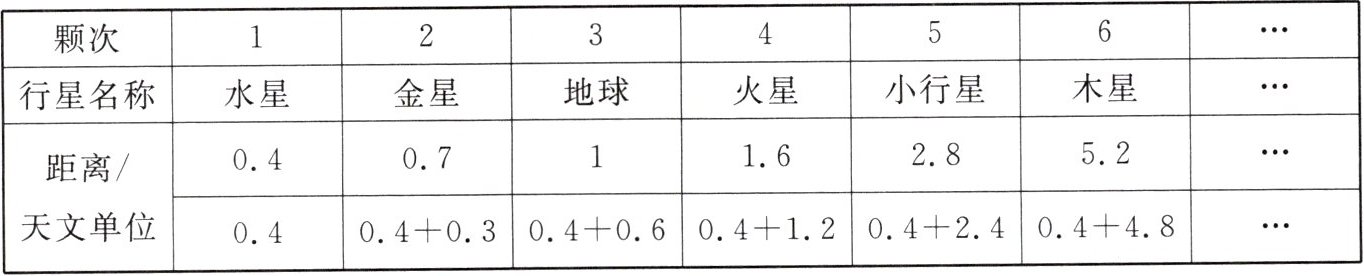
那么第 7 颗行星到太阳的距离是(
A.7 天文单位
B.8 天文单位
C.9 天文单位
D.10 天文单位

那么第 7 颗行星到太阳的距离是(
D
)。A.7 天文单位
B.8 天文单位
C.9 天文单位
D.10 天文单位
答案:
D
3. 已知 $9×1 + 0 = 9$,$9×2 + 1 = 19$,$9×3 + 2 = 29$,$9×4 + 3 = 39$,…,按此规律,第 6 个式子是
9×6+5=59
。
答案:
9×6+5=59
4. 观察下面的单项式:$a$,$-2a^{2}$,$4a^{3}$,$-8a^{4}$,…,根据你发现的规律,第 8 个式子是
-128a⁸
。
答案:
-128a⁸
查看更多完整答案,请扫码查看


