《2025年配套综合练习甘肃七年级数学上册北师大版》

5. 下列结论正确的是(A)。
A.绝对值大于 $ 1 $ 的数的平方一定大于 $ 1 $
B.一个数的立方一定大于这个数
C.任何小于 $ 1 $ 的数的平方都小于原数
D.一个数的平方一定大于这个数

答案： A

6. 已知 $ x,y $ 是有理数,且满足 $ (x + 4)^{2} + |y - 2| = 0 $,则 $ x^{y} $ 的值是16。

答案： 16

7. 阅读材料：若 $ a^{b}= N(a＞0 $,且 $ a \neq 1) $,则 $ b = \log_{a}N $,称 $ b $ 是以 $ a $ 为底 $ N $ 的对数,例如 $ 2^{3}= 8 $,则 $ \log_{2}8 = \log_{2}2^{3} = 3 $。根据材料填空：$ \log_{3}9 = $2。

答案： 2

8. 计算：
(1) $ (-6)^{3} $；
(2) $ \left(-\dfrac{3}{2}\right)^{2} $；
(3) $ -\dfrac{2^{2}}{3} $。

答案：
(1)-216
(2)$\frac{9}{4}$
(3)$-\frac{4}{3}$

9. 如果 $ 0 ＜ a ＜ 1 $,那么 $ a^{2},a,\dfrac{1}{a} $ 之间的大小关系是(B)。
A.$ a ＜ a^{2} ＜ \dfrac{1}{a} $
B.$ a^{2} ＜ a ＜ \dfrac{1}{a} $
C.$ \dfrac{1}{a} ＜ a ＜ a^{2} $
D.$ \dfrac{1}{a} ＜ a^{2} ＜ a $

答案： B

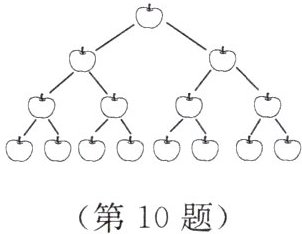
10. 如图所示的是一幅“苹果图”,第一行有 $ 1 $ 个苹果,第二行有$ 2 $ 个,第三行有 $ 4 $ 个,第四行有 $ 8 $ 个······你能否发现苹果的排列规律？猜猜看,第十行有512个苹果。

答案： 512

11. 计算：
(1) $ (-2)^{3}×(-3)^{2} $；
(2) $ (-3)^{2}÷(-2^{4}) $；
(3) $ \left(\dfrac{3}{4}\right)^{3}÷\left(-\dfrac{3}{2}\right)^{3} $。

答案： 解:
(1)原式=(-8)×9=-72。
(2)原式=9÷(-16)=$-\frac{9}{16}$。
(3)原式=$\frac{27}{64}÷(-\frac{27}{8})=\frac{27}{64}×(-\frac{8}{27})=-\frac{1}{8}$。

12. 已知 $ 2^{1}= 2,2^{2}= 4,2^{3}= 8,2^{4}= 16,2^{5}= 32,… $。观察前面式子,试猜想 $ 2^{204} $ 的末位数字,并说明理由。

答案： 解:$2^{204}$的末位数字是6。理由如下:204÷4=51,又由题知,$2^n$的末位数字以2,4,8,6循环,$2^{204}$的末位数字恰好是第4个,所以$2^{204}$的末位数字是6。