第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 成反比例的两个量具有怎样的关系?
2. 你能举出一些生活中成反比例关系的例子吗?
2. 你能举出一些生活中成反比例关系的例子吗?
答案:
1. 解:成反比例的两个量,它们的乘积是一个定值。即若两个量$x$、$y$成反比例,则$xy = k$($k$为常数,$k\neq0$)。
2. 解:生活中成反比例关系的例子有:
路程一定时,速度和时间成反比例。比如从学校到家的路程$s$是固定的,速度$v$越快,所用时间$t$就越短,且$v× t=s$($s$为常数)。
长方形面积一定时,长和宽成反比例。若长方形面积$S$固定,长$a$越长,宽$b$就越短,且$a× b = S$($S$为常数)。
2. 解:生活中成反比例关系的例子有:
路程一定时,速度和时间成反比例。比如从学校到家的路程$s$是固定的,速度$v$越快,所用时间$t$就越短,且$v× t=s$($s$为常数)。
长方形面积一定时,长和宽成反比例。若长方形面积$S$固定,长$a$越长,宽$b$就越短,且$a× b = S$($S$为常数)。
1. 某实践小组完成活动后,要把一篇3000字的社会调查报告录入电脑.
(1) 若有3个同学计划完成录入的时间分别是20分钟、25分钟、30分钟,则他们录入文字的速度分别是多少字/分?
(2) 分别用$x$ (单位:分)和$y$ (单位:字/分)表示录入文字时间和录入文字速度,用式子表示$y与x$的关系,$y与x$成什么比例关系?
【思路分析】问题中涉及录入文字字数、录入文字时间及录入文字速度这三个量,它们之间具有关系:录入文字字数 = 录入文字速度×录入文字时间,录入文字速度 = $\frac{录入文字字数}{录入文字时间}$.
【解答】(1) 3个同学录入文字的速度分别是$\frac{3000}{20}= 150$ (字/分 ), $\frac{3000}{25}= 120$ (字/分 ), $\frac{3000}{30}= 100$ (字/分 ).
(2) $xy = 3000或y = \frac{3000}{x}$, $y与x$成反比例关系.
(1) 若有3个同学计划完成录入的时间分别是20分钟、25分钟、30分钟,则他们录入文字的速度分别是多少字/分?
(2) 分别用$x$ (单位:分)和$y$ (单位:字/分)表示录入文字时间和录入文字速度,用式子表示$y与x$的关系,$y与x$成什么比例关系?
【思路分析】问题中涉及录入文字字数、录入文字时间及录入文字速度这三个量,它们之间具有关系:录入文字字数 = 录入文字速度×录入文字时间,录入文字速度 = $\frac{录入文字字数}{录入文字时间}$.
【解答】(1) 3个同学录入文字的速度分别是$\frac{3000}{20}= 150$ (字/分 ), $\frac{3000}{25}= 120$ (字/分 ), $\frac{3000}{30}= 100$ (字/分 ).
(2) $xy = 3000或y = \frac{3000}{x}$, $y与x$成反比例关系.
答案:
(1)$150$字/分,$120$字/分,$100$字/分;
(2)$y=\frac{3000}{x}$,反比例关系。
(2)$y=\frac{3000}{x}$,反比例关系。
2. 已知杠杆平衡条件为:阻力×阻力臂 = 动力×动力臂(如图3.1 - 1).
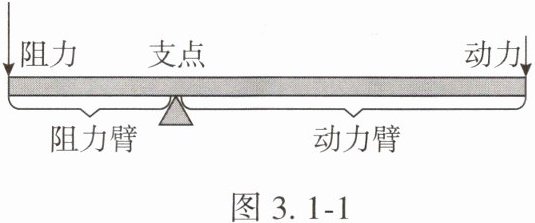
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.动力$F(N)与动力臂l(m)$的数据如表3.1 - 2:
|动力$F/N$|0.5|1|
|动力臂$l/m$|

(1) 填写表3.1 - 2,用式子表示动力$F与动力臂l$的关系,$F与l$成什么比例关系?
(2) 动力$F是怎样随动力臂l$的变化而变化的?当动力臂为3m时,撬动石头至少需要多大的力?小伟只有500N的力量,他该选择动力臂为多少的撬棍才能撬动这块大石头呢?
【思路分析】根据物理学知识,当阻力与阻力臂的乘积确定时,动力$F与动力臂l$的乘积也是确定的,所以两者成反比例关系.
【解答】(1) 如表3.1 - 3.
|动力$F/N$|0.5|1|1.5|2|…|
|动力臂$l/m$|1200|600|400|300|…|

$F = $
(2) 动力$F随动力臂l$的变大而变小.
因为$F = \frac{600}{l}$,所以$F = \frac{600}{3}= $
当动力臂为3m时,撬动石头至少需要
因为$Fl = 600$,所以$500l = 600$,所以$l = $
小伟只有500N的力量,他该选择动力臂至少为

小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.动力$F(N)与动力臂l(m)$的数据如表3.1 - 2:
|动力$F/N$|0.5|1|
1.5
|2
|…||动力臂$l/m$|
1200
|600
|400|300|…|
(1) 填写表3.1 - 2,用式子表示动力$F与动力臂l$的关系,$F与l$成什么比例关系?
(2) 动力$F是怎样随动力臂l$的变化而变化的?当动力臂为3m时,撬动石头至少需要多大的力?小伟只有500N的力量,他该选择动力臂为多少的撬棍才能撬动这块大石头呢?
【思路分析】根据物理学知识,当阻力与阻力臂的乘积确定时,动力$F与动力臂l$的乘积也是确定的,所以两者成反比例关系.
【解答】(1) 如表3.1 - 3.
|动力$F/N$|0.5|1|1.5|2|…|
|动力臂$l/m$|1200|600|400|300|…|

$F = $
$\frac{600}{l}$
, $F与l$成反比例
关系.(2) 动力$F随动力臂l$的变大而变小.
因为$F = \frac{600}{l}$,所以$F = \frac{600}{3}= $
200
.当动力臂为3m时,撬动石头至少需要
200
N的力.因为$Fl = 600$,所以$500l = 600$,所以$l = $
1.2
.小伟只有500N的力量,他该选择动力臂至少为
1.2
m的撬棍才能撬动这块大石头.
答案:
答题卡:
(1)
|动力$F/N$| $0.5$| $1$| $1.5$| $2$| $\cdots$|
|---|---|---|---|---|---|
|动力臂$l/m$| $1200$| $600$| $400$| $300$| $\cdots$|
$F=\frac{600}{l}$,$F$与$l$成反比例关系。
(2) 动力$F$随动力臂$l$的变大而变小。
当$l = 3m$时,$F=\frac{600}{3}=200N$,撬动石头至少需要$200N$的力。
由$Fl = 600$,$500l = 600$,得$l = 1.2m$,小伟该选择动力臂至少为$1.2m$的撬棍才能撬动这块大石头。
(1)
|动力$F/N$| $0.5$| $1$| $1.5$| $2$| $\cdots$|
|---|---|---|---|---|---|
|动力臂$l/m$| $1200$| $600$| $400$| $300$| $\cdots$|
$F=\frac{600}{l}$,$F$与$l$成反比例关系。
(2) 动力$F$随动力臂$l$的变大而变小。
当$l = 3m$时,$F=\frac{600}{3}=200N$,撬动石头至少需要$200N$的力。
由$Fl = 600$,$500l = 600$,得$l = 1.2m$,小伟该选择动力臂至少为$1.2m$的撬棍才能撬动这块大石头。
查看更多完整答案,请扫码查看


