第37页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
9. 如图甲所示为两个光滑的斜面,AC大于BC,将同一物体分别沿AC、BC以一定的速度从底部匀速拉到顶点C,运动快慢的图像如图乙所示,施加的力分别为F1、F2,且平行于各自斜面向上,拉力的功率分别为P1、P2,则F1______F2,P1______P2。(填“>”“<”或“=”)
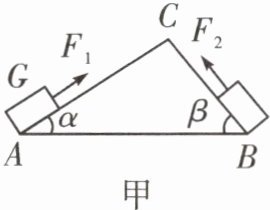
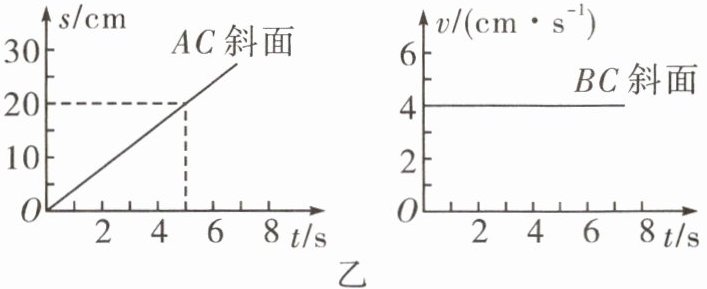


答案:
$<$;$<$
10. 学校新近买了总质量为300 kg的30套科学实验器材,每套一箱。现在某实验员需要把这批实验器材搬运到14 m高的科学实验室。
(1)该实验员需要做多少功?(不考虑他克服自身重力所做的功,g取10 N/kg)
(2)假设他身体可以提供的功率P(如图所示)取决于所搬运物体的质量m。若要尽可能快地把这批器材搬上去,则他每次搬运的箱子数应为______个。
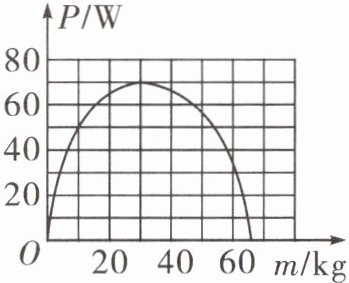
(3)不考虑搬起箱子、放下箱子和下楼时间,求他搬运这批实验器材的最短时间。
(1)该实验员需要做多少功?(不考虑他克服自身重力所做的功,g取10 N/kg)
(2)假设他身体可以提供的功率P(如图所示)取决于所搬运物体的质量m。若要尽可能快地把这批器材搬上去,则他每次搬运的箱子数应为______个。

(3)不考虑搬起箱子、放下箱子和下楼时间,求他搬运这批实验器材的最短时间。
答案:
(1) 42000 J
(2) 3
(3) 600 s
(1) 42000 J
(2) 3
(3) 600 s
11. 如图所示,轻质杠杆OP长1 m,能绕O点转动,P端用细绳悬于N点。现有一重力为10 N的物体A通过滑环挂在M点,OM段的长度为10 cm。由于杆OP与水平方向成30°角,滑环刚好能由M点向P端匀速滑动,滑动速度为2 cm/s,细绳PN能承受的最大拉力为5 N。问:
(1)滑环从M点开始滑动,经过多长时间后,细绳PN会断裂?
(2)从滑环自M点滑动到绳PN断裂时,物体A所受重力做的功是多少?
(3)上述过程中,物体A所受重力做功的功率是多少?
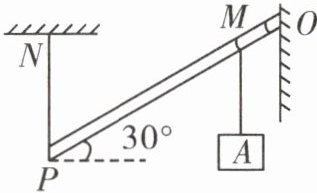
(1)滑环从M点开始滑动,经过多长时间后,细绳PN会断裂?
(2)从滑环自M点滑动到绳PN断裂时,物体A所受重力做的功是多少?
(3)上述过程中,物体A所受重力做功的功率是多少?

答案:
(1)解:设滑环滑动时间为$t$,则滑环到$O$点的距离$L = 0.1m + 0.02m/s × t$。根据杠杆平衡条件$F_{PN} × OP × \cos30^{\circ} = G × L × \cos30^{\circ}$,即$5N × 1m = 10N × L$,解得$L = 0.5m$。所以$0.1m + 0.02m/s × t = 0.5m$,解得$t = 20s$。
(2)解:滑环移动距离$s = vt = 0.02m/s × 20s = 0.4m$,物体A下降高度$h = s × \sin30^{\circ} = 0.4m × 0.5 = 0.2m$,重力做功$W = Gh = 10N × 0.2m = 2J$。
(3)解:功率$P = \frac{W}{t} = \frac{2J}{20s} = 0.1W$。
(1)20s;
(2)2J;
(3)0.1W
(1)解:设滑环滑动时间为$t$,则滑环到$O$点的距离$L = 0.1m + 0.02m/s × t$。根据杠杆平衡条件$F_{PN} × OP × \cos30^{\circ} = G × L × \cos30^{\circ}$,即$5N × 1m = 10N × L$,解得$L = 0.5m$。所以$0.1m + 0.02m/s × t = 0.5m$,解得$t = 20s$。
(2)解:滑环移动距离$s = vt = 0.02m/s × 20s = 0.4m$,物体A下降高度$h = s × \sin30^{\circ} = 0.4m × 0.5 = 0.2m$,重力做功$W = Gh = 10N × 0.2m = 2J$。
(3)解:功率$P = \frac{W}{t} = \frac{2J}{20s} = 0.1W$。
(1)20s;
(2)2J;
(3)0.1W
查看更多完整答案,请扫码查看


