搜索
7. 在下午四点半时,时针和分针所夹的角度是(
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$
45°
)A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$
答案：
B【解析】下午四点半，时针和分针中间相差1.5个大格.因为钟表12个数字，每相邻两个数字之间的夹角为30°，所以下午四点半时分针与时针的夹角是1.5×30°=45°.
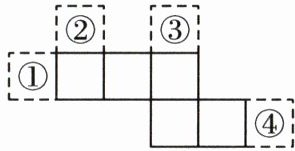
8. 在图中的①②③④的任意一个位置放置一个小正方形后所组成的图形能折成一个正方体,那么可放置的位置不能是(
A.①
B.②
C.③
D.④
A
)A.①
B.②
C.③
D.④
答案：
A【解析】将小正方形放在②③④中的任意一个位置后所组成的图形均能折成正方体，放在①处时，折叠后有两个面重叠，不能折成正方体.
9. 如果线段 $AB = 5\mathrm{cm}$,线段 $BC = 4\mathrm{cm}$,那么 A,C 两点之间的距离是(
A.$9\mathrm{cm}$
B.$1\mathrm{cm}$
C.$1\mathrm{cm}$ 或 $9\mathrm{cm}$
D.以上答案都不对
D
)A.$9\mathrm{cm}$
B.$1\mathrm{cm}$
C.$1\mathrm{cm}$ 或 $9\mathrm{cm}$
D.以上答案都不对
答案：
D【解析】
(1)当A，B，C三点在一条直线上时，分点B在A，C之间和点C在A，B之间两种情况讨论.①当点B在A，C之间时，AC=AB+BC=5+4=9(cm)；②当点C在A，B之间时，AC=AB - BC=5 - 4=1(cm).所以A，C两点间的距离是9 cm或1 cm.
(2)当A，B，C三点不在一条直线上时，A，C两点之间的距离有多种可能.
(1)当A，B，C三点在一条直线上时，分点B在A，C之间和点C在A，B之间两种情况讨论.①当点B在A，C之间时，AC=AB+BC=5+4=9(cm)；②当点C在A，B之间时，AC=AB - BC=5 - 4=1(cm).所以A，C两点间的距离是9 cm或1 cm.
(2)当A，B，C三点不在一条直线上时，A，C两点之间的距离有多种可能.
10. 如图,$\angle AOB = 120^{\circ}$,射线 OC 在平面内. 射线 OC 绕点 O 从图中位置(此时点 A,O,C 在一条直线上)出发,逆时针旋转角 $\alpha(0^{\circ} \lt \alpha \lt 180^{\circ})$,已知 OM 平分 $\angle AOC$,当 $\angle MOC$ 与 $\angle BOC$ 互余时旋转角 $\alpha$ 等于( )
A.$30^{\circ}$ 或 $105^{\circ}$
B.$30^{\circ}$ 或 $120^{\circ}$
C.$40^{\circ}$ 或 $105^{\circ}$
D.$40^{\circ}$ 或 $120^{\circ}$
A.$30^{\circ}$ 或 $105^{\circ}$
B.$30^{\circ}$ 或 $120^{\circ}$
C.$40^{\circ}$ 或 $105^{\circ}$
D.$40^{\circ}$ 或 $120^{\circ}$
答案：
D【解析】如图①，当射线OC在∠AOB外部时，由题意可得∠AOC=180° - α，∠BOC=180° - α - 120°=60° - α.因为OM是∠AOC的平分线，所以∠MOC=$\frac{1}{2}$∠AOC=90° - $\frac{1}{2}$α，因为∠MOC+∠BOC=90°，所以90° - $\frac{1}{2}$α+60° - α=90°，所以α=40°；
如图②，当射线OC在∠AOB内部时，由题意可得∠AOC=180° - α，∠BOC=∠AOB - ∠AOC=120° - (180° - α)=α - 60°，因为OM是∠AOC的平分线，所以∠MOC=$\frac{1}{2}$∠AOC=90° - $\frac{1}{2}$α，因为∠MOC+∠BOC=90°，所以90° - $\frac{1}{2}$α+α - 60°=90°，所以α=120°.综上，α=40°或α=120°.
D【解析】如图①，当射线OC在∠AOB外部时，由题意可得∠AOC=180° - α，∠BOC=180° - α - 120°=60° - α.因为OM是∠AOC的平分线，所以∠MOC=$\frac{1}{2}$∠AOC=90° - $\frac{1}{2}$α，因为∠MOC+∠BOC=90°，所以90° - $\frac{1}{2}$α+60° - α=90°，所以α=40°；
如图②，当射线OC在∠AOB内部时，由题意可得∠AOC=180° - α，∠BOC=∠AOB - ∠AOC=120° - (180° - α)=α - 60°，因为OM是∠AOC的平分线，所以∠MOC=$\frac{1}{2}$∠AOC=90° - $\frac{1}{2}$α，因为∠MOC+∠BOC=90°，所以90° - $\frac{1}{2}$α+α - 60°=90°，所以α=120°.综上，α=40°或α=120°. 11. 计算：$16^{\circ}24' + 21^{\circ}40' = $
38°4′
.
答案：
38°4′【解析】原式=37°64′=38°4′.
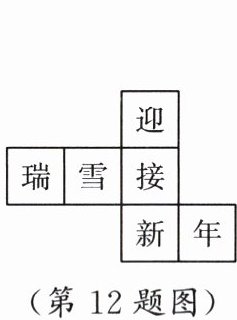
12. 一个正方体的展开图如图所示,将它折叠成正方体后“雪”字对面的字是
年
.
答案：
年【解析】将它折叠成正方体后“雪”字对面的字是“年”.
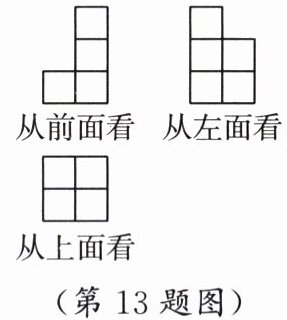
13. 王老师将 n 盒粉笔整齐地摞在讲桌上,从三个方向看到的平面图形如图所示,则 n 的值是
7
.
答案：
7【解析】从前面看到的图形有2列，每列中正方形的个数分别为1和3，故从上面看到的图形中，左列的两个正方形中分别记上1，1，右列的两个正方形中分别记上3，3；从左面看到的图形有2列，每列中正方形的个数分别为3，2，故从上面看到的图形中，上面一行的两个正方形中分别记上3，3，下面一行的两个正方形中分别记上2，2.取从上面看到的图形中每个正方形中较小的数字相加，得n=1+3+2+1=7.
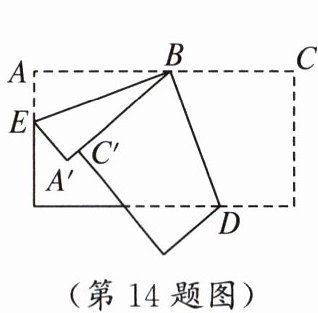
14. 如图,将一张长方形纸片按图中的方式折叠,BD,BE 为折痕,若 $\angle ABE = 20^{\circ}$,则 $\angle CBD = $
70°
.
答案：
70°【解析】由题意可知∠ABE=∠EBA′，∠A′BD=∠DBC，因为∠ABE=20°，所以∠CBD=$\frac{1}{2}$∠A′BC=$\frac{1}{2}$(180° - ∠ABA′)=$\frac{1}{2}$×(180° - 2∠ABE)=$\frac{1}{2}$×(180° - 2×20°)=70°.
15. 已知 A,B,C 三点在同一条直线上,若 $AB = 20$,$AC = 30$,则线段 BC 的长度为______.
答案：
10或50【解析】如图①，当点C在线段AB的延长线上时，因为AB=20，AC=30，BC=AC - AB，所以BC=10；
如图②，当点C在线段BA延长线上时， 
因为AB=20，AC=30，BC=AC+AB，所以BC=50.故线段BC的长度为10或50.
10或50【解析】如图①，当点C在线段AB的延长线上时，因为AB=20，AC=30，BC=AC - AB，所以BC=10；
如图②，当点C在线段BA延长线上时， 因为AB=20，AC=30，BC=AC+AB，所以BC=50.故线段BC的长度为10或50. 16. 如图,C 为直线 AB 上一点,$\angle DCE$ 为直角,CF 平分 $\angle ACD$,CH 平分 $\angle BCD$,CG 平分 $\angle BCE$,则以下结论：① $\angle ACF$ 与 $\angle DCH$ 互余；② $\angle HCG = 60^{\circ}$；③ $\angle ECF$ 与 $\angle BCH$ 互补；④ $\angle ACF - \angle BCG = 45^{\circ}$. 其中正确的为______.(填序号)
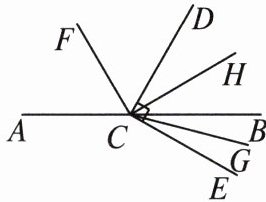
①③④
答案：
①③④【解析】因为CF平分∠ACD，CH平分∠BCD，CG平分∠BCE，所以∠ACF=∠FCD=$\frac{1}{2}$∠ACD，∠DCH=∠HCB=$\frac{1}{2}$∠DCB，∠BCG=∠ECG=$\frac{1}{2}$∠BCE.因为∠ACB=180°，∠DCE=90°，所以∠FCH=∠FCD+∠DCH=$\frac{1}{2}$(∠ACD+∠BCD)=$\frac{1}{2}$×180°=90°，∠HCG=∠HCB+∠BCG=$\frac{1}{2}$(∠BCD+∠BCE)=$\frac{1}{2}$∠DCE=$\frac{1}{2}$×90°=45°，所以∠FCG=∠FCH+∠HCG=90°+45°=135°.所以∠ACF+∠DCH=∠DCF+∠DCH=∠FCH=90°，故①正确，②错误.因为∠ECF=∠DCE+∠FCD=90°+∠FCD，∠FCD+∠DCH=90°，所以∠ECF+∠DCH=180°，因为∠DCH=∠HCB，所以∠ECF与∠BCH互补，故③正确.因为∠ACD - ∠BCE=180° - ∠DCB - ∠BCE=90°，所以∠ACF - ∠BCG=45°，故④正确.
查看更多完整答案，请扫码查看
