16. 如图 22 - 6 所示,某大桥有一段抛物线形的拱梁,抛物线的解析式为 $ y= ax^{2}+bx $. 小强骑自行车从拱梁一端 $ O $ 沿直线匀速穿过拱梁部分的桥面 $ OC $,当小强骑自行车行驶 $ 10 $ s 时和 $ 26 $ s 时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面 $ OC $ 共需______s.


答案:
36 解析:设在10 s时到达A点,在26 s时到达B点,因为10 s时和26 s时拱梁的高度相同,所以A,B两点关于对称轴对称.从O点到A点需要10 s,则从B点到C点需要10 s,所以从O点到C点需要$26+10=36(s)$.
17. (10 分)已知函数 $ y= mx^{2}-6x + 1 $($ m $ 是常数).
(1)求证:不论 $ m $ 为何值,该函数的图象都经过 $ y $ 轴上的一个定点;
(2)若该函数的图象与 $ x $ 轴只有一个交点,求 $ m $ 的值.
(1)求证:不论 $ m $ 为何值,该函数的图象都经过 $ y $ 轴上的一个定点;
(2)若该函数的图象与 $ x $ 轴只有一个交点,求 $ m $ 的值.
答案:
(1)证明:因为当$x=0$时,$y=1$,所以不论m为何值,函数$y=mx^2-6x+1$的图象都经过y轴上的定点$(0,1)$.
(2)解:①当$m=0$时,函数$y=-6x+1$的图象与x轴只有一个交点;②当$m\neq0$时,若函数$y=mx^2-6x+1$的图象与x轴只有一个交点,则方程$mx^2-6x+1=0$有两个相等的实数根,所以$\Delta=(-6)^2-4m=0$,所以$m=9$.综上,若函数$y=mx^2-6x+1$的图象与x轴只有一个交点,则m的值为0或9.
(1)证明:因为当$x=0$时,$y=1$,所以不论m为何值,函数$y=mx^2-6x+1$的图象都经过y轴上的定点$(0,1)$.
(2)解:①当$m=0$时,函数$y=-6x+1$的图象与x轴只有一个交点;②当$m\neq0$时,若函数$y=mx^2-6x+1$的图象与x轴只有一个交点,则方程$mx^2-6x+1=0$有两个相等的实数根,所以$\Delta=(-6)^2-4m=0$,所以$m=9$.综上,若函数$y=mx^2-6x+1$的图象与x轴只有一个交点,则m的值为0或9.
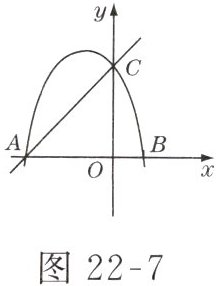
18. (12 分)如图 22 - 7 所示,抛物线 $ y= -x^{2}-2x + 3 $ 与 $ x $ 轴交于点 $ A $ 和点 $ B $,与 $ y $ 轴交于点 $ C $.
(1)求点 $ A $,$ B $,$ C $ 的坐标;
(2)求直线 $ AC $ 的解析式;
(3)设点 $ M $ 是第二象限内抛物线上的一点,且 $ S_{\triangle MAB}= 6 $,求点 $ M $ 的坐标.
(1)求点 $ A $,$ B $,$ C $ 的坐标;
(2)求直线 $ AC $ 的解析式;
(3)设点 $ M $ 是第二象限内抛物线上的一点,且 $ S_{\triangle MAB}= 6 $,求点 $ M $ 的坐标.

答案:
(1)令$-x^2-2x+3=0$,即$(x+3)(x-1)=0$,故$x_1=-3,x_2=1$,故$A(-3,0),B(1,0)$.令$x=0$,则$y=3$,故$C(0,3)$.
(2)设直线AC的解析式为$y=kx+b$,由题意,得$\begin{cases}-3k+b=0,\\b=3,\end{cases}$解得$\begin{cases}k=1,\\b=3,\end{cases}$故$y=x+3$.
(3)设点M的坐标为$(x,-x^2-2x+3)$,因为点M在第二象限,所以$-x^2-2x+3>0$.又因为$AB=4$,所以$\frac{1}{2}×4×(-x^2-2x+3)=6$,解得$x=0$或$x=-2$.当$x=0$时,$y=3$(不合题意);当$x=-2$时,$y=3$,所以点M的坐标为$(-2,3)$.
(1)令$-x^2-2x+3=0$,即$(x+3)(x-1)=0$,故$x_1=-3,x_2=1$,故$A(-3,0),B(1,0)$.令$x=0$,则$y=3$,故$C(0,3)$.
(2)设直线AC的解析式为$y=kx+b$,由题意,得$\begin{cases}-3k+b=0,\\b=3,\end{cases}$解得$\begin{cases}k=1,\\b=3,\end{cases}$故$y=x+3$.
(3)设点M的坐标为$(x,-x^2-2x+3)$,因为点M在第二象限,所以$-x^2-2x+3>0$.又因为$AB=4$,所以$\frac{1}{2}×4×(-x^2-2x+3)=6$,解得$x=0$或$x=-2$.当$x=0$时,$y=3$(不合题意);当$x=-2$时,$y=3$,所以点M的坐标为$(-2,3)$.
查看更多完整答案,请扫码查看


