第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
3. 切线长及其定理
(1) 概念:经过圆外一点的圆的切线上,这点和
(2) 定理:从圆外一点可以引圆的
(1) 概念:经过圆外一点的圆的切线上,这点和
切点
之间线段的长,叫作这点到圆的切线长。(2) 定理:从圆外一点可以引圆的
两
条切线,它们的切线长相等
,这一点和圆心的连线平分
两条切线的夹角。
答案:
(1)切点
(2)两 相等 平分
(1)切点
(2)两 相等 平分
4. 三角形的内切圆
(1) 与三角形各边都相切的圆叫作三角形的
(2) 三角形内切圆的圆心是三角形
(1) 与三角形各边都相切的圆叫作三角形的
内切圆
。(2) 三角形内切圆的圆心是三角形
三条角平分线
的交点,叫作三角形的内心
,它到三角形三边
的距离相等。
答案:
(1)内切圆
(2)三条角平分线 内心 三边
(1)内切圆
(2)三条角平分线 内心 三边
5. 根据预习内容,回答问题。
已知$PA$,$PB是\odot O$的切线,$A$,$B$是切点,如果$\angle AOB = 136^{\circ}$,那么$\angle P = $
已知$PA$,$PB是\odot O$的切线,$A$,$B$是切点,如果$\angle AOB = 136^{\circ}$,那么$\angle P = $
$44^{\circ}$
。
答案:
$44^{\circ}$ 解析:因为$PA$,$PB$是$\odot O$的切线,所以$OA\perp PA$,$OB\perp PB$.在四边形$PAOB$中,$\angle PAO=\angle PBO = 90^{\circ}$,所以$\angle AOB+\angle P = 180^{\circ}$,所以$\angle P = 180^{\circ}-\angle AOB = 44^{\circ}$.
1. 从圆外一点向半径为$9$的圆作切线,若切线长为$18$,则从这一点到圆的最短距离为( )
A.$9\sqrt{3}$
B.$9(\sqrt{3} - 1)$
C.$9(\sqrt{5} - 1)$
D.$9$
A.$9\sqrt{3}$
B.$9(\sqrt{3} - 1)$
C.$9(\sqrt{5} - 1)$
D.$9$
答案:
C 解析:如图D - 24 - 18所示,因为$PA$切$\odot O$于点$A$,
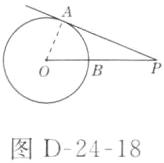
所以$\angle OAP = 90^{\circ}$,$PA = 18$,$OA = 9$,所以$PO=\sqrt{18^{2}+9^{2}} = 9\sqrt{5}$,所以$PB = 9\sqrt{5}-9 = 9(\sqrt{5}-1)$.
C 解析:如图D - 24 - 18所示,因为$PA$切$\odot O$于点$A$,

所以$\angle OAP = 90^{\circ}$,$PA = 18$,$OA = 9$,所以$PO=\sqrt{18^{2}+9^{2}} = 9\sqrt{5}$,所以$PB = 9\sqrt{5}-9 = 9(\sqrt{5}-1)$.
2. 如图24-2-22所示,$PA$,$PB是\odot O$的切线,$AC是\odot O$的直径,$\angle P = 40^{\circ}$,则$\angle BAC = $
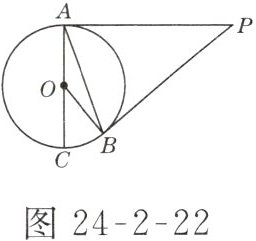
$20^{\circ}$
。
答案:
$20^{\circ}$ 解析:因为$PA$,$PB$是$\odot O$的切线,所以$PA = PB$,$\angle PAC = 90^{\circ}$,所以$\angle PAB=\angle PBA=\frac{180^{\circ}-\angle P}{2}=70^{\circ}$,所以$\angle BAC=\angle PAC-\angle PAB = 90^{\circ}-70^{\circ}=20^{\circ}$.
3. 如图24-2-23所示,$I是\triangle ABC$的内心,$\angle A = 80^{\circ}$,求$\angle BIC$的度数。


答案:
解:因为$\angle A = 80^{\circ}$,所以$\angle ABC+\angle ACB = 100^{\circ}$.因为$I$是$\triangle ABC$的内心,所以$\angle IBC=\frac{1}{2}\angle ABC$,$\angle ICB=\frac{1}{2}\angle ACB$.所以$\angle IBC+\angle ICB=\frac{1}{2}(\angle ABC+\angle ACB)=50^{\circ}$.所以$\angle BIC = 180^{\circ}-50^{\circ}=130^{\circ}$.
4. 如图24-2-24所示,$PA$,$PB分别是\odot O$的切线,$A$,$B$是切点,$\angle OAB = 30^{\circ}$。
(1) 求$\angle APB$的度数;
(2) 当$OA = 3$时,求$AP$的长。

(1) 求$\angle APB$的度数;
(2) 当$OA = 3$时,求$AP$的长。

答案:
解:
(1)因为$PA$,$PB$是$\odot O$的切线,所以$PA = PB$,$OA\perp PA$.又$\angle OAB = 30^{\circ}$所以$\angle BAP = 90^{\circ}-30^{\circ}=60^{\circ}$.所以$\triangle ABP$是等边三角形,所以$\angle APB = 60^{\circ}$.
(2)如图D - 24 - 19所示,连接$OP$.
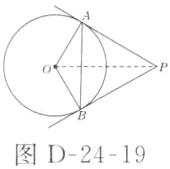
因为$PA$,$PB$分别是$\odot O$的切线,所以$PO$平分$\angle APB$,即$\angle APO=\frac{1}{2}\angle APB = 30^{\circ}$.在$Rt\triangle OAP$中,$OA = 3$,$\angle APO = 30^{\circ}$,所以$OP = 2OA = 6$.由勾股定理得$AP=\sqrt{OP^{2}-OA^{2}} = 3\sqrt{3}$.
解:
(1)因为$PA$,$PB$是$\odot O$的切线,所以$PA = PB$,$OA\perp PA$.又$\angle OAB = 30^{\circ}$所以$\angle BAP = 90^{\circ}-30^{\circ}=60^{\circ}$.所以$\triangle ABP$是等边三角形,所以$\angle APB = 60^{\circ}$.
(2)如图D - 24 - 19所示,连接$OP$.

因为$PA$,$PB$分别是$\odot O$的切线,所以$PO$平分$\angle APB$,即$\angle APO=\frac{1}{2}\angle APB = 30^{\circ}$.在$Rt\triangle OAP$中,$OA = 3$,$\angle APO = 30^{\circ}$,所以$OP = 2OA = 6$.由勾股定理得$AP=\sqrt{OP^{2}-OA^{2}} = 3\sqrt{3}$.
查看更多完整答案,请扫码查看


