第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
4. 设$\odot O的半径为r$,圆心到直线$l的距离为d$。可得
(1) 直线$l和\odot O相交\Leftrightarrow$
(2) 直线$l和\odot O相切\Leftrightarrow$
(3) 直线$l和\odot O相离\Leftrightarrow$
(1) 直线$l和\odot O相交\Leftrightarrow$
①$d<r$
;(2) 直线$l和\odot O相切\Leftrightarrow$
②$d=r$
;(3) 直线$l和\odot O相离\Leftrightarrow$
③$d>r$
。
答案:
①$d<r$ ②$d=r$ ③$d>r$
5. 根据预习内容,回答问题。
直线和圆有公共点,则直线和圆的位置关系是(
A.相交
B.相切
C.相交或相切
D.无法确定
直线和圆有公共点,则直线和圆的位置关系是(
C
)A.相交
B.相切
C.相交或相切
D.无法确定
答案:
C
1. 已知$\odot O的面积为9\pi cm^{2}$,若点$O到直线l的距离为\pi cm$,则直线$l与\odot O$的位置关系是(
A.相交
B.相切
C.相离
D.无法确定
C
)A.相交
B.相切
C.相离
D.无法确定
答案:
C 解析:设$\odot O$的半径为$r\ cm$,则$\pi r^{2}=9\pi$,故$r = 3$.因为$\pi>3$,所以直线$l$与$\odot O$的位置关系是相离.
2. 直线$l与半径为r的\odot O$相交,且点$O到直线l的距离为5$,则半径$r$的取值范围是(
A.$r > 5$
B.$r = 5$
C.$0 < r < 5$
D.$0 < r \leq 5$
A
)A.$r > 5$
B.$r = 5$
C.$0 < r < 5$
D.$0 < r \leq 5$
答案:
A
3. 已知$\odot O的直径为12 cm$,如果圆心$O到直线a的距离为5 cm$,那么直线$a与\odot O$有
2
个公共点。
答案:
2 解析:因为$\odot O$的半径为$6\ cm$,且$5<6$,所以直线$a$与$\odot O$相交,故直线与$\odot O$有两个公共点.
4. 如图24-2-6所示,$\odot O的半径OD为5 cm$,直线$l \perp OD$,垂足为$O$,则直线$l沿射线OD$方向平移
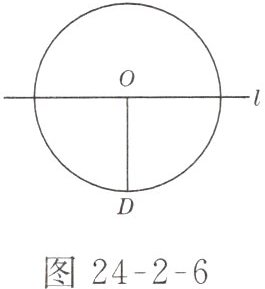
5
$cm时与\odot O$相切。
答案:
5
5. 已知$\odot O的圆心O到直线l的距离为d$,$\odot O的半径为r$,若$d$,$r是关于x的方程x^{2} - 4x + m = 0$的两个根,且直线$l与\odot O$相切,则$m$的值为
4
。
答案:
4 解析:因为直线$l$与$\odot O$相切,所以$d = r$.所以方程$x^{2}-4x + m = 0$有两个相等实根.所以$(-4)^{2}-4m = 0$.解得$m = 4$.
6. 已知$\angle AOB = 30^{\circ}$,$M为OB$上一点,且$OM = 5 cm$,以点$M$为圆心,以$r为半径的圆与直线OA$有怎样的位置关系?为什么?
(1) $r = 2 cm$;(2) $r = 4 cm$;(3) $r = 2.5 cm$。
(1) $r = 2 cm$;(2) $r = 4 cm$;(3) $r = 2.5 cm$。
答案:
解:如图D - 24 - 13所示,过点$M$作$MN\perp OA$于点$N$.
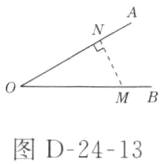
因为$\angle AOB = 30^{\circ}$,所以$MN=\frac{1}{2}OM=\frac{1}{2}×5 = 2.5(cm)$.
(1)当$r = 2\ cm$时,因为$2.5>2$,所以$\odot M$与$OA$相离.
(2)当$r = 4\ cm$时,因为$2.5<4$,所以$\odot M$与$OA$相交.
(3)当$r = 2.5\ cm$时,因为$2.5 = 2.5$,所以$\odot M$与$OA$相切.
解:如图D - 24 - 13所示,过点$M$作$MN\perp OA$于点$N$.

因为$\angle AOB = 30^{\circ}$,所以$MN=\frac{1}{2}OM=\frac{1}{2}×5 = 2.5(cm)$.
(1)当$r = 2\ cm$时,因为$2.5>2$,所以$\odot M$与$OA$相离.
(2)当$r = 4\ cm$时,因为$2.5<4$,所以$\odot M$与$OA$相交.
(3)当$r = 2.5\ cm$时,因为$2.5 = 2.5$,所以$\odot M$与$OA$相切.
1. 已知$\odot O的半径为\sqrt{5} cm$,圆心$O到直线l的距离为d$,如果直线$l与\odot O$有公共点,那么(
A.$d > \sqrt{5} cm$
B.$d = \sqrt{5} cm$
C.$0 cm \leq d < \sqrt{5} cm$
D.$0 cm \leq d \leq \sqrt{5} cm$
D
)A.$d > \sqrt{5} cm$
B.$d = \sqrt{5} cm$
C.$0 cm \leq d < \sqrt{5} cm$
D.$0 cm \leq d \leq \sqrt{5} cm$
答案:
D
2. $OA平分\angle BOC$,$P是OA$上任意一点(点$O$除外),若以点$P为圆心的\odot P与OC$相离,则$\odot P与OB$的位置关系是(
A.相离
B.相切
C.相交
D.相交或相切
A
)A.相离
B.相切
C.相交
D.相交或相切
答案:
A 解析:角平分线上的点到角两边的距离相等.
查看更多完整答案,请扫码查看


