第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
4. 根据预习内容,回答问题.
已知点 $A$ 的坐标为 $(-1,2)$,则点 $A$ 关于 $x$ 轴对称的点的坐标为
已知点 $A$ 的坐标为 $(-1,2)$,则点 $A$ 关于 $x$ 轴对称的点的坐标为
(-1,-2)
,关于 $y$ 轴对称的点的坐标为(1,2)
,关于原点对称的点的坐标为(1,-2)
.
答案:
(-1,-2) (1,2) (1,-2)
1. 若点 $A(n,2)$ 与 $B(-3,m)$ 关于原点对称,则 $n - m$ 等于(
A.$-1$
B.$-5$
C.$1$
D.$5$
D
)A.$-1$
B.$-5$
C.$1$
D.$5$
答案:
D 解析:由题意可得n+(-3)=0,2+m=0,解得n=3,m=-2.所以n-m=3-(-2)=5.
2. 设点 $P(x,y)$ 在第二象限,且 $|x| = 2$,$|y| = 3$,则点 $P$ 关于原点的对称点的坐标是(
A.$(-2,3)$
B.$(-3,2)$
C.$(3,-2)$
D.$(2,-3)$
D
)A.$(-2,3)$
B.$(-3,2)$
C.$(3,-2)$
D.$(2,-3)$
答案:
D 解析:因为|x|=2,|y|=3,所以x=±2,y=±3.又因为点P(x,y)在第二象限,所以x<0,y>0.所以x=-2,y=3.所以点P(-2,3)关于原点的对称点是(2,-3).
3. 已知坐标原点 $O$ 是平行四边形 $ABCD$ 对角线 $AC$,$BD$ 的交点,若点 $A(1,-2)$,点 $B(3,4)$,则点 $C$ 的坐标为
(-1,2)
,点 $D$ 的坐标为(-3,-4)
.
答案:
(-1,2) (-3,-4) 解析:平行四边形ABCD是中心对称图形,对称中心是对角线AC,BD的交点,即点A与点C关于原点对称.所以点C的坐标为(-1,2).同理,点D的坐标为(-3,-4).
4. 已知点 $A(2a + 2,3 - 3b)$ 与点 $B(2b - 4,3a + 6)$ 关于坐标原点对称,求 $a$ 与 $b$ 的值.
答案:
解:因为点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,则{2a+2+2b-4=0,3-3b+3a+6=0,解得{a=-1,b=2.
1. 已知点 $A$ 的坐标为 $(2,2)$,如果点 $A$ 关于 $x$ 轴的对称点是 $B$,点 $B$ 关于原点的对称点是 $C$,那么点 $C$ 的坐标是(
A.$(2,2)$
B.$(-2,2)$
C.$(2,-2)$
D.$(-2,-2)$
(-2,2)
)A.$(2,2)$
B.$(-2,2)$
C.$(2,-2)$
D.$(-2,-2)$
答案:
B 解析:由题意得,点B的坐标为(2,-2),所以点C的坐标为(-2,2).
2. 如图 23-2-14 所示,将一朵小花放置在平面直角坐标系中第三象限内的甲位置,先将它绕原点 $O$ 旋转 $180^{\circ}$ 到乙位置,再将它向下平移 $2$ 个单位长度到丙位置,则小花顶点 $A$ 在丙位置中的对应点 $A'$ 的坐标为(
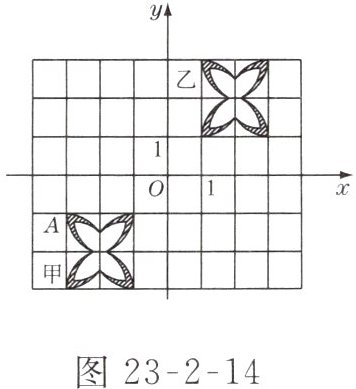
A.$(3,1)$
B.$(1,3)$
C.$(3,-1)$
D.$(1,1)$
C
)
A.$(3,1)$
B.$(1,3)$
C.$(3,-1)$
D.$(1,1)$
答案:
C 解析:点A(-3,-1)关于原点的对称点坐标为(3,1),再向下平移2个单位长度,则横坐标不变,纵坐标减2,所以点A'的坐标为(3,-1).
3. 已知菱形 $ABCD$ 在平面直角坐标系中的位置如图 23-2-15 所示,若 $AD$ 边的中点 $P$ 的坐标为 $(1.5,2)$,则 $BC$ 边的中点 $Q$ 的坐标是(
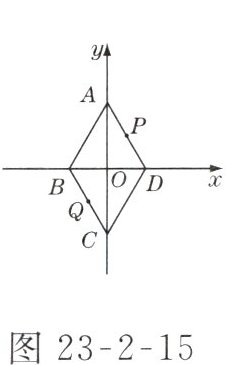
A.$(-1.5,-2)$
B.$(-2,-1.5)$
C.$(-3,-2)$
D.$(-3,-4)$
A
)
A.$(-1.5,-2)$
B.$(-2,-1.5)$
C.$(-3,-2)$
D.$(-3,-4)$
答案:
A 解析:菱形是中心对称图形,其对称中心为坐标原点.所以P,Q两点关于原点对称,所以Q点坐标为(-1.5,-2).
4. 如图 23-2-16 所示,若将 $\triangle ABC$ 绕点 $C$ 顺时针旋转 $90^{\circ}$ 后得到 $\triangle A'B'C$,则点 $A$ 对应点 $A'$ 的坐标是(
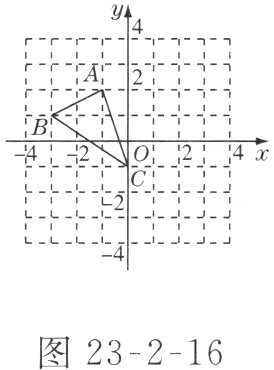
A.$(-3,-2)$
B.$(2,2)$
C.$(3,0)$
D.$(2,1)$
C
)
A.$(-3,-2)$
B.$(2,2)$
C.$(3,0)$
D.$(2,1)$
答案:
C 解析:在方格中作∠ACA'=90°,且CA'=CA=√10,可知点A'的坐标为(3,0).
5. 若 $\triangle ABC$ 与 $\triangle EFC$ 关于点 $C$ 中心对称,并且 $A$ 与 $E$ 是对称点,则四边形 $ABEF$ 是
平行四边
形.
答案:
平行四边 解析:根据中心对称的性质可得AC=CE,BC=CF,即四边形ABEF对角线互相平分,所以是平行四边形.
6. 若点 $P(-2,a)$ 与点 $P'(2,b)$ 关于原点中心对称,则 $a + b$ 的值为
0
.
答案:
0 解析:直接利用关于原点中心对称的点的坐标特征得a+b=0.
查看更多完整答案,请扫码查看


