《2025年阳光课堂金牌练习册九年级数学上册人教版》

5. 如图23-1-8所示,以左边图案的圆心为旋转中心,将图案按顺时针方向旋转$90^{\circ}$即可得到右边的图案.

答案： 顺时针 $90^{\circ}$

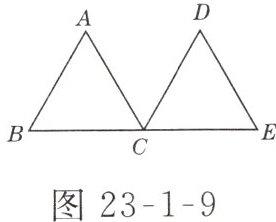
6. 如图23-1-9所示,等边△ABC绕点C顺时针旋转120°后得到△EDC,那么点A的对应点是点E；线段AB的对应线段是ED；∠B的对应角是∠D；∠A的对应角是∠E；旋转中心是点C.

答案： E $ED$ $\angle D$ $\angle E$ 点$C$

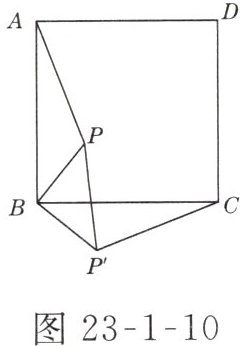
7. 如图23-1-10所示,点P是正方形ABCD内一点,△ABP经旋转能与△CBP'重合.
(1)旋转中心是哪个点？
(2)旋转了多少度？
(3)若PB= 3,求△PBP'的面积.

答案： 解:
(1)旋转中心是点$B$.
(2)顺时针旋转了$90^{\circ}$.
(3)因为$\triangle ABP$经旋转能与$\triangle CBP'$重合,所以$BP=BP'=3$,$\angle ABP=\angle CBP'$,所以$\angle CBP'+\angle PBC=\angle ABP+\angle PBC=\angle ABC=90^{\circ}$,即$\angle PBP'=90^{\circ}$,所以$S_{\triangle PBP'}=\frac{1}{2}BP\cdot BP'=\frac{1}{2}× 3× 3=4.5$.

1. 把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称。

答案： 重合

2. 把一个平面图形绕着平面内某一点O转动一个角度,叫作图形的旋转。

答案： 绕着平面内某一点O

3. 轴对称的性质：如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。

答案： 垂直平分线

4. 把一个图形绕着某一点旋转$180^{\circ }$,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫作对称中心。这两个图形在旋转后能重合的对应点叫作关于对称中心的对称点。

答案： $180^{\circ }$ 对称中心 对称点

5. 中心对称的性质：中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分；中心对称的两个图形是全等图形。

答案： 对称中心 平分 全等图形

6. 根据预习内容,回答问题。
如果$\triangle ABC和\triangle A'B'C'关于点O$中心对称,那么$\triangle ABC和\triangle A'B'C'$形状相同,大小相等,即它们是全等关系。

答案： 形状 相等 全等