《2025年阳光课堂金牌练习册九年级数学上册人教版》

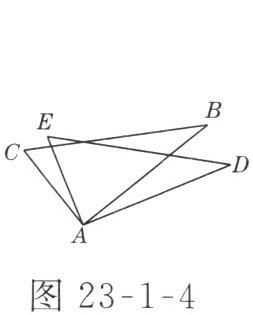
3. 如图23-1-4所示,△ABC绕着点A旋转能够与△ADE完全重合,则下列结论成立的有(C)
①AE= AC；②∠CAE= ∠BAD；③BC//AD；④若连接BD,则△ABD为等腰三角形.

A.1个
B.2个
C.3个
D.4个

答案： C 解析:根据旋转的性质可知$AE=AC$,$AB=AD$,$\angle CAE=\angle BAD$,故正确的结论有①②④,故选C.

4. 如图23-1-5所示,若△ABC绕点A顺时针旋转得到△AED,则旋转角是$\angle BAE$(或$\angle CAD$). 若△ABC的周长是12cm,面积是$6cm^2,$则△AED的周长是$12\ cm$,面积是$6\ cm^2$.

答案： $\angle BAE$(或$\angle CAD$) $12\ cm$ $6\ cm^2$ 解析:因为旋转中心已经知道,所以根据一对对应点观察,很容易确定旋转角,再根据旋转的性质:"旋转前、后的图形全等"可得$\triangle AED$的周长、面积与$\triangle ABC$的周长、面积分别相等.

5. 如图23-1-6所示,将一个含有30°角的直角三角板ABC绕点B顺时针旋转得到Rt△A'BC',且点A,B,C'在一条直线上.
(1)指出旋转中心,求出旋转角的度数；
(2)说出对应角和对应线段.

答案： 解:
(1)旋转中心为点$B$,旋转角的度数为$120^{\circ}$.
(2)对应角:$\angle A$与$\angle A'$,$\angle C$与$\angle C'$,$\angle ABC$与$\angle A'BC'$; 对应线段:$AB$与$A'B$,$AC$与$A'C'$,$BC$与$BC'$.

1. △ABC绕点A旋转后得到△AFE,已知∠BAC= 70°,则∠EAF的度数是(B)
A.50°
B.70°
C.130°
D.110°

答案： B

2. 下列图形中,△ABC经过旋转之后不能得到△A'B'C'的是(D)

答案： D 解析:A,B,C三项经过旋转之后都能得到$\triangle A'B'C'$,只有D不能,它是通过翻折得到的.

3. 下列图形旋转90°能与自身重合的是(D)

答案： D

4. 如图23-1-7,如果△ABC经旋转后能与△A'B'C重合,已知∠ACB= 60°,那么哪一点是旋转中心,旋转了多少度？(A)

A.点C,逆时针旋转90°
B.点C,顺时针旋转90°
C.点B,逆时针旋转30°
D.点B,逆时针旋转90°

答案： A