《2025年阳光课堂金牌练习册九年级数学上册人教版》

6. 从地面垂直向上抛一小球,小球的高度$h$(单位：$m$)与小球运动时间$t$(单位：$s$)的函数关系式是$h = 9.8t - 4.9t^{2}$,那么小球运动中的最大高度为4.9$m$.

答案： 4.9

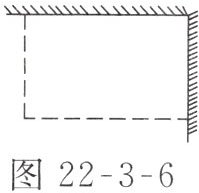
7. 如图22-3-6所示,用长为$18\ m$的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
(1)设矩形的一边长为$x$(单位：$m$),面积为$y$(单位：$m^{2}$),求$y关于x$的函数解析式,并写出自变量$x$的取值范围.
(2)当$x$为何值时,所围苗圃的面积最大,最大面积是多少？

答案： 解:
(1)$y=x(18-x)=-x^{2}+18x(0＜x＜18)$.
(2)$y=-x^{2}+18x(0＜x＜18)$.因为$a=-1＜0$,所以$y$有最大值.故当$x=-\dfrac{18}{2×(-1)}=9$时,$y_{最大值}=\dfrac{0-18^{2}}{4×(-1)}=81(m^{2})$,即当$x=9$时,所围苗圃的面积最大,最大面积是$81\ m^{2}$.

8. 我国某地的跨江大桥采用了国际上新颖的$V$型钢构组合拱桥结构,主桥的钢拱在空中划出一道优美的弧线,远远望去像是一弯彩虹横卧于清波之上. 大桥的桥拱是抛物线的一部分,位于桥面上方部分的拱高为$20\ m$,跨度为$120\ m$(如图22-3-7所示).
(1)请你建立适当的直角坐标系,求出可以近似描述主桥上的钢拱形状的函数解析式；
(2)距离桥拱与桥面交点$20\ m$处的支架长为多少米？

答案： 解:
(1)建立如图D-22-5所示的平面直角坐标系.设所求函数解析式为$y=ax^{2}+20$,代入点$(60,0)$的坐标,得$0=60^{2}a+20$,解得$a=-\dfrac{1}{180}$.故所求函数的解析式为$y=-\dfrac{1}{180}x^{2}+20$.
(2)设距离桥拱与桥面交点20m处的点的坐标是$(40,y)$,则$y=-\dfrac{1}{180}×40^{2}+20=\dfrac{100}{9}(m)$.故距离桥拱与桥面交点20m处的支架长为$\dfrac{100}{9}\ m$.
点拨:建立的直角坐标系以方便解题为原则,建立的直角坐标系不同,求出的函数解析式也不同.