《2025年阳光课堂金牌练习册九年级数学上册人教版》

1. 列一元二次方程解实际问题的一般步骤：审、设、列、解、验、答.

答案： 审 设 列 解 验 答

3. 有关利润的公式：
利润=售价-进价=进价×利润率,
总利润=单个商品的利润×销售量,
利润率=利润/进价×100%.

答案： 售价-进价 利润率 单个商品的利润 销售量 利润/进价

4. 一般地,当$a＞0(a＜0)$时,抛物线$y = ax^{2}+bx + c$的顶点是最低(高)点,也就是说,当$x = $$-\dfrac{b}{2a}$时,二次函数$y = ax^{2}+bx + c$有最小(大)值$\dfrac{4ac-b^{2}}{4a}$.

答案： $-\dfrac{b}{2a}$ $\dfrac{4ac-b^{2}}{4a}$

5. 根据预习内容,回答问题.
当$x = $$-\dfrac{3}{4}$时,二次函数$y= -2x^{2}-3x + 2$有最大值为$\dfrac{25}{8}$.

答案： $-\dfrac{3}{4}$ 大 $\dfrac{25}{8}$

1. 为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为$100\ m$,则池底的最大面积是(625)
A.$600\ m^{2}$
B.$625\ m^{2}$
C.$650\ m^{2}$
D.$675\ m^{2}$

答案： B 解析:设矩形的一边长为$x\ m$,则其邻边长为$(50-x)\ m$.设矩形的面积为$S\ m^{2}$,则$S=x(50-x)=-x^{2}+50x=-(x-25)^{2}+625$.因为$-1＜0$,所以$S$有最大值,最大值为625.

2. 有一种工艺品,每件进价为$100$元,当标价为$135$元时,每天可售出$100$件,根据销售统计,一件工艺品每降价$1$元出售,则每天可多售出$4$件. 要使每天获得的利润最大,每件需降价(A)
A.$5$元
B.$10$元
C.$0$元
D.$36$元

答案： A 解析:设每件需降价$x$元,每天的利润为$y$元,由题意得$y=(35-x)(100+4x)=-4x^{2}+40x+3500=-4(x-5)^{2}+3600$.因为$-4＜0$,所以$y$有最大值,当$x=5$时,最大值为3600.

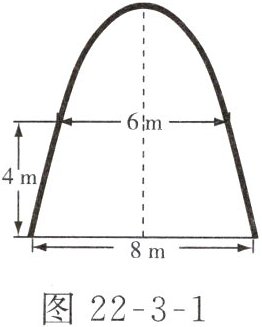
3. 某大学的校门是一抛物线形水泥建筑物,如图22-3-1所示(示意图),大门的地面宽度为$8\ m$,两侧距地面$4\ m$高处各有一个挂校名横匾用的铁环,两铁环的水平距离为$6\ m$,则校门的高为(精确到$0.1\ m$,水泥建筑物厚度忽略不计)(B)

A.$9.2\ m$
B.$9.1\ m$
C.$9\ m$
D.$5.1\ m$

答案： B 解析:以地面为$x$轴,抛物线的对称轴为$y$轴建立直角坐标系,由题意可设抛物线解析式为$y=ax^{2}+k$.因为抛物线过点$(4,0)$,$(3,4)$,所以$\begin{cases}16a+k=0,\\9a+k=4,\end{cases}$解得$\begin{cases}a=-\dfrac{4}{7},\\k=\dfrac{64}{7}.\end{cases}$所以校门的高度为$\dfrac{64}{7}\approx9.1(m)$.