《2025年阳光课堂金牌练习册九年级数学上册人教版》

1. 在下列四个图案中,既是轴对称图形又是中心对称图形的是( )

答案： B　解析:A项是中心对称图形,C项既不是中心对称图形，也不是轴对称图形，D项是轴对称图形.

2. 抛物线 $ y = -3x^2 - x + 4 $ 与坐标轴的交点的个数是( )

A.3
B.2
C.1
D.0

答案： A　解析:根据抛物线与一元二次方程之间的关系得,$b^{2}-4ac=(-1)^{2}-4×(-3)×4=1+48＞0$,故抛物线$y=-3x^{2}-x+4$与x轴有两个交点.又因为抛物线与y轴交于点$(0,4)$,故抛物线$y=-3x^{2}-x+4$与坐标轴有3个交点.

3. 下列事件：①在足球赛中,弱队战胜强队；②抛掷一枚硬币,落地后正面朝上；③任取两个正整数,其和大于1；④长分别为3,5,9厘米的三条线段能围成一个三角形. 其中确定性事件的个数是( )

A.1
B.2
C.3
D.4

答案： B　解析:确定性事件就是一定发生的事件或一定不会发生的事件.根据定义即可确定:①②属于随机事件，③是必然事件，④是不可能事件,所以属于确定性事件的个数是2.

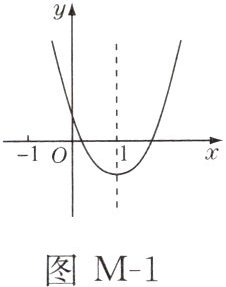
4. 二次函数 $ y = ax^2 + bx + c $ 的图象如图M-1所示,则下列关系式错误的是( )

A.$ a ＞ 0 $
B.$ c ＞ 0 $
C.$ b^2 - 4ac ＞ 0 $
D.$ a + b + c ＞ 0 $

答案： D　解析:因为抛物线开口向上，所以$a＞0$,所以A项正确;因为抛物线与y轴的交点在x轴上方，所以$c＞0$,所以B项正确;因为抛物线与x轴有两个交点，所以$b^{2}-4ac＞0$,所以C项正确;因为抛物线的对称轴是直线$x=1$,顶点在x轴下方，所以当$x=1$时,$y=a+b+c＜0$,所以D项错误.

5. 在一个不透明的袋子中,有2个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出1个球记下颜色放回,再随机地摸出1个球,则2次都摸到白球的概率为( )

A.$ \frac{1}{16} $



B.$ \frac{1}{8} $
C.$ \frac{1}{4} $
D.$ \frac{1}{2} $

答案：
C　解析:画树状图，如图D - M - 1所示.
　　　　　
所有可能的结果共有16种，其中两次都摸到白球的有4种，所以P(两次都摸到白球)=$\frac{4}{16}=\frac{1}{4}$.

6. 已知：如图M-2所示,$ \odot O $ 的割线 $ PAB $ 交 $ \odot O $ 于点 $ A $,$ B $,$ PA = 7 cm $,$ AB = 5 cm $,$ OP = 10 cm $,则 $ \odot O $ 的半径是( )

A.4 cm
B.5 cm
C.6 cm
D.7 cm

答案： A　解析:连接OA,过点O作$OD⊥AB$于点D(图略).由垂径定理得$AD=\frac{1}{2}AB = 2.5(cm)$.在$Rt△OPD$和$Rt△OAD$中,由勾股定理,得$OD^{2}=OP^{2}-PD^{2}=OA^{2}-AD^{2}$,所以$10^{2}-9.5^{2}=OA^{2}-2.5^{2}$,所以$OA^{2}=16$,所以$OA = 4cm$.

7. 如图M-3所示,一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面圆半径是( )

A.1
B.$ \frac{3}{4} $
C.$ \frac{1}{2} $
D.$ \frac{1}{3} $

答案： C　解析:设圆锥的底面圆半径为r,则有$2πr = π$,所以$r=\frac{1}{2}$.