8. 两个转盘如图25-1所示,如果指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是( )
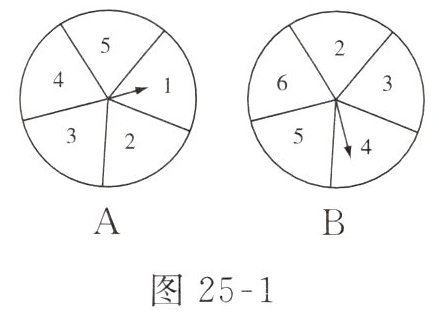
A.$\frac{19}{25}$
B.$\frac{10}{25}$
C.$\frac{6}{25}$
D.$\frac{5}{25}$

A.$\frac{19}{25}$
B.$\frac{10}{25}$
C.$\frac{6}{25}$
D.$\frac{5}{25}$
答案:
C
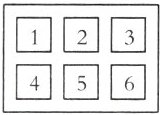
9. 如图25-2所示,每一个标有数字的方块均是可以翻动的木牌,其中只有两块木牌的背面贴有中奖的标志,则随机翻动一块木牌中奖的概率为______.

答案:
$\frac{1}{3}$ 解析:P(中奖)=$\frac{2}{6}$=$\frac{1}{3}$.
10. 掷一枚均匀正方体骰子,出现点数为4的概率为______,出现点数为2的概率为______,出现点数大于3的概率为______,出现点数大于2的概率为______.
答案:
$\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{2}$ $\frac{2}{3}$
11. 在100张奖券中,设一等奖1个,二等奖2个,三等奖3个. 若从中任取一张奖券,则不中奖的概率是______.
答案:
$\frac{47}{50}$ 解析:P(不中奖)=$\frac{100−1−2−3}{100}$=$\frac{94}{100}$=$\frac{47}{50}$.
12. 某暗箱中放有10个球,其中有红球3个,白球和蓝球若干,从中任取一个球是白球的概率是$\frac{1}{2}$,则白球和蓝球的个数分别是______,______.
答案:
5 2 解析:白球:10×$\frac{1}{2}$=5(个),蓝球:10−5−3=2(个).
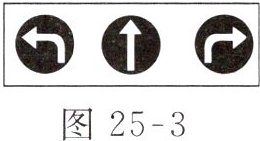
13. 如图25-3所示,在某十字路口,汽车可直行、可左转、可右转. 若这三种可能性相同,则两辆汽车经过该路口都向右转的概率为______.

答案:
$\frac{1}{9}$ 解析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两辆汽车经过该路口都向右转的结果,继而利用概率公式即可求得答案.
画树状图,如图PC−25−1所示.

所有可能的结果共有9种,其中两辆汽车经过该路口都向右转的有1种,
所以两辆汽车经过该路口都向右转的概率为$\frac{1}{9}$.
$\frac{1}{9}$ 解析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两辆汽车经过该路口都向右转的结果,继而利用概率公式即可求得答案.
画树状图,如图PC−25−1所示.

所有可能的结果共有9种,其中两辆汽车经过该路口都向右转的有1种,
所以两辆汽车经过该路口都向右转的概率为$\frac{1}{9}$.
14. 一套书共有上、中、下三册,将它们任意摆放到书架的同一层上,这三册书从左到右恰好成上、中、下顺序的概率为______.
答案:
$\frac{1}{6}$ 解析:列出从左到右的所有排列顺序如下:上、中、下;上、下、中;中、上、下;中、下、上;下、中、上;下、上、中.所以从左到右恰好成上、中、下顺序的概率是$\frac{1}{6}$.
15. (10分)一个袋中共有5个除颜色外其他均相同的红球和白球,若任意摸出一球为红球的概率是$\frac{2}{5}$.
(1)袋中红球、白球各有多少个?
(2)任意摸出两个球,它们均为红球的概率有多大?
(1)袋中红球、白球各有多少个?
(2)任意摸出两个球,它们均为红球的概率有多大?
答案:
解:
(1)5×$\frac{2}{5}$=2(个),5−2=3(个),
即袋中有2个红球,3个白球.
(2)画出树状图,如图PC−25−2所示.

由图可知,P(摸出两个球都是红球)=$\frac{2}{20}$=$\frac{1}{10}$.
解:
(1)5×$\frac{2}{5}$=2(个),5−2=3(个),
即袋中有2个红球,3个白球.
(2)画出树状图,如图PC−25−2所示.

由图可知,P(摸出两个球都是红球)=$\frac{2}{20}$=$\frac{1}{10}$.
查看更多完整答案,请扫码查看


