16. (10 分)如图 24-12 所示,线段$AB与\odot O相切于点C$,连接$OA$,$OB$,$OB交\odot O于点D$,已知$OA = OB = 6$,$AB = 6\sqrt{3}$.
(1) 求$\odot O$的半径;
(2) 求图中阴影部分的面积.

(1) 求$\odot O$的半径;
(2) 求图中阴影部分的面积.

答案:
分析:
(1)连接OC,在$Rt\triangle AOC$中,利用勾股定理求得OC;
(2)$S_{阴影}=S_{\triangle OCB}-S_{扇形OCD}$.解:
(1)连接OC(图略).因为AB切$\odot O$于点C,所以$OC\perp AB$.因为$OA=OB$,所以$AC=BC=\frac{1}{2}AB=3\sqrt{3}$.在$Rt\triangle AOC$中,$OC=\sqrt{OA^2-AC^2}=\sqrt{6^2-(3\sqrt{3})^2}=3$,所以$\odot O$的半径为3.
(2)因为在$Rt\triangle OCB$中,$OC=3$,$OB=6$,所以$OC=\frac{1}{2}OB$,所以$\angle COD=60°$,所以$S_{扇形OCD}=\frac{60×\pi×3^2}{360}=\frac{3}{2}\pi$,所以$S_{阴影}=S_{\triangle OBC}-S_{扇形OCD}=\frac{1}{2}OC\cdot CB-\frac{3}{2}\pi=\frac{9\sqrt{3}}{2}-\frac{3}{2}\pi$.
(1)连接OC,在$Rt\triangle AOC$中,利用勾股定理求得OC;
(2)$S_{阴影}=S_{\triangle OCB}-S_{扇形OCD}$.解:
(1)连接OC(图略).因为AB切$\odot O$于点C,所以$OC\perp AB$.因为$OA=OB$,所以$AC=BC=\frac{1}{2}AB=3\sqrt{3}$.在$Rt\triangle AOC$中,$OC=\sqrt{OA^2-AC^2}=\sqrt{6^2-(3\sqrt{3})^2}=3$,所以$\odot O$的半径为3.
(2)因为在$Rt\triangle OCB$中,$OC=3$,$OB=6$,所以$OC=\frac{1}{2}OB$,所以$\angle COD=60°$,所以$S_{扇形OCD}=\frac{60×\pi×3^2}{360}=\frac{3}{2}\pi$,所以$S_{阴影}=S_{\triangle OBC}-S_{扇形OCD}=\frac{1}{2}OC\cdot CB-\frac{3}{2}\pi=\frac{9\sqrt{3}}{2}-\frac{3}{2}\pi$.
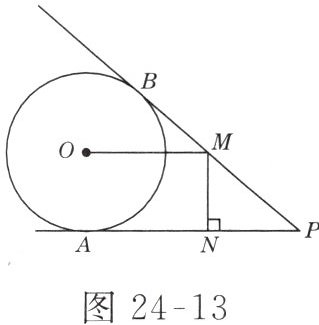
17. (12 分)如图 24-13 所示,$PA$,$PB分别与\odot O相切于点A$,$B$,点$M在PB$上,且$OM // AP$,$MN \perp AP$,垂足为$N$.
(1) 求证:$OM = AN$.
(2) 若$\odot O的半径R = 3$,$PA = 9$,求$OM$的长.
(1) 求证:$OM = AN$.
(2) 若$\odot O的半径R = 3$,$PA = 9$,求$OM$的长.

答案:
分析:
(1)连接OA,证四边形ANMO是矩形,得$OM=AN$;
(2)连接OB,可证$OM=MP$,设$OM=x$,则$NP=9-x$,在$Rt\triangle MNP$中利用勾股定理列方程求x.
(1)证明:如图PC-24-2所示,连接OA,则$OA\perp AP$.因为$MN\perp AP$,所以$MN// OA$.因为$OM// AP$,所以四边形ANMO是矩形.所以$OM=AN$.
(2)解:连接OB,则$OB\perp BP$.因为$OA=MN$,$OA=OB$,$OM// AP$,所以$OB=MN$,$\angle OMB=\angle NPM$.所以$Rt\triangle OBM\congRt\triangle MNP$,所以$OM=MP$.设$OM=x$,则$NP=9-x$.在$Rt\triangle MNP$中,有$x^2=3^2+(9-x)^2$,所以$x=5$,即$OM=5$.
(1)连接OA,证四边形ANMO是矩形,得$OM=AN$;
(2)连接OB,可证$OM=MP$,设$OM=x$,则$NP=9-x$,在$Rt\triangle MNP$中利用勾股定理列方程求x.
(1)证明:如图PC-24-2所示,连接OA,则$OA\perp AP$.因为$MN\perp AP$,所以$MN// OA$.因为$OM// AP$,所以四边形ANMO是矩形.所以$OM=AN$.
(2)解:连接OB,则$OB\perp BP$.因为$OA=MN$,$OA=OB$,$OM// AP$,所以$OB=MN$,$\angle OMB=\angle NPM$.所以$Rt\triangle OBM\congRt\triangle MNP$,所以$OM=MP$.设$OM=x$,则$NP=9-x$.在$Rt\triangle MNP$中,有$x^2=3^2+(9-x)^2$,所以$x=5$,即$OM=5$.
查看更多完整答案,请扫码查看


