14. (10 分)如图 24-10 所示,$AB是\odot O$的一条弦,$OD \perp AB于点C$,交$\odot O于点D$,点$E在\odot O$上.
(1) 若$\angle AOD = 52^{\circ}$,求$\angle DEB$的度数.
(2) 若$OC = 3$,$OA = 5$,求$AB$的长.
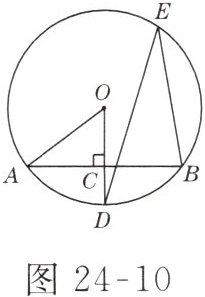
(1) 若$\angle AOD = 52^{\circ}$,求$\angle DEB$的度数.
(2) 若$OC = 3$,$OA = 5$,求$AB$的长.

答案:
解:
(1)因为$OD\perp AB$,所以$AC=BC$,$\overset{\frown}{AD}=\overset{\frown}{BD}$.所以$\angle DEB=\frac{1}{2}\angle AOD=\frac{1}{2}×52°=26°$.
(2)在$Rt\triangle OAC$中,$AC=\sqrt{OA^2-OC^2}=\sqrt{5^2-3^2}=4$,所以$AB=2AC=8$.
(1)因为$OD\perp AB$,所以$AC=BC$,$\overset{\frown}{AD}=\overset{\frown}{BD}$.所以$\angle DEB=\frac{1}{2}\angle AOD=\frac{1}{2}×52°=26°$.
(2)在$Rt\triangle OAC$中,$AC=\sqrt{OA^2-OC^2}=\sqrt{5^2-3^2}=4$,所以$AB=2AC=8$.
15. (10 分)如图 24-11 所示,在$\triangle ABC$中,$D是AB$边上一点,$\odot O过D$,$B$,$C$三点,$\angle DOC = 2\angle ACD = 90^{\circ}$.
(1) 求证:直线$AC是\odot O$的切线;
(2) 如果$\angle ACB = 75^{\circ}$,$\odot O$的半径为 2,求$BD$的长.

(1) 求证:直线$AC是\odot O$的切线;
(2) 如果$\angle ACB = 75^{\circ}$,$\odot O$的半径为 2,求$BD$的长.

答案:
(1)证明:因为$OD=OC$,$\angle DOC=90°$,所以$\angle ODC=\angle OCD=45°$.因为$\angle DOC=2\angle ACD=90°$,所以$\angle ACD=45°$.所以$\angle ACD+\angle OCD=\angle OCA=90°$.因为点C在$\odot O$上,所以直线AC是$\odot O$的切线.
(2)解:因为$OD=OC=2$,$\angle DOC=90°$,所以$CD=2\sqrt{2}$.因为$\angle ACB=75°$,$\angle ACD=45°$,所以$\angle BCD=30°$.如图PC-24-1所示,过点D作$DE\perp BC$于点E,则$\angle DEC=90°$.所以$DE=\frac{1}{2}CD=\sqrt{2}$.因为$\angle B=\frac{1}{2}\angle COD=45°$,所以$BD=\sqrt{2}DE=2$.
(1)证明:因为$OD=OC$,$\angle DOC=90°$,所以$\angle ODC=\angle OCD=45°$.因为$\angle DOC=2\angle ACD=90°$,所以$\angle ACD=45°$.所以$\angle ACD+\angle OCD=\angle OCA=90°$.因为点C在$\odot O$上,所以直线AC是$\odot O$的切线.
(2)解:因为$OD=OC=2$,$\angle DOC=90°$,所以$CD=2\sqrt{2}$.因为$\angle ACB=75°$,$\angle ACD=45°$,所以$\angle BCD=30°$.如图PC-24-1所示,过点D作$DE\perp BC$于点E,则$\angle DEC=90°$.所以$DE=\frac{1}{2}CD=\sqrt{2}$.因为$\angle B=\frac{1}{2}\angle COD=45°$,所以$BD=\sqrt{2}DE=2$.
查看更多完整答案,请扫码查看


