《2025年阳光课堂金牌练习册九年级数学上册人教版》

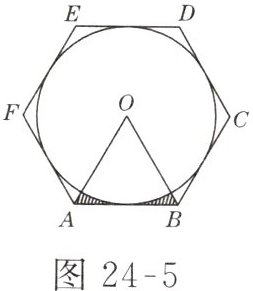
6. 如图 24-5 所示,$\odot O的外切正六边形ABCDEF$的边长为 2,则图中阴影部分的面积为( )

A.$\sqrt{3} - \frac{\pi}{2}$
B.$\sqrt{3} - \frac{2\pi}{3}$


C.$2\sqrt{3} - \frac{\pi}{2}$
D.$2\sqrt{3} - \frac{2\pi}{3}$

答案： A 解析:因为六边形ABCDEF是正六边形,所以$\angle AOB=60°$.又因为$OA=OB$,所以$\triangle OAB$是等边三角形,$OA=OB=AB=2$.设点G为AB与$\odot O$的切点,OA,OB分别交$\odot O$于M,N两点,连接OG(图略),则$OG\perp AB$.在$Rt\triangle OAG$中,$OA=2$,$AG=1$,根据勾股定理得$OG=\sqrt{OA^2-AG^2}=\sqrt{3}$.$S_{阴影}=S_{\triangle OAB}-S_{扇形OMN}=\frac{1}{2}×2×\sqrt{3}-\frac{60×\pi×(\sqrt{3})^2}{360}=\sqrt{3}-\frac{\pi}{2}$.

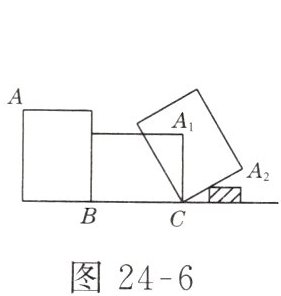
7. 如图 24-6 所示,有一长为 4 cm,宽为 3 cm 的长方形木板在桌面上无滑动翻滚(顺时针方向),木板上的顶点$A的位置变化为A \to A_1 \to A_2$,其中第二次翻滚被桌面上一小木块挡住,使木板边沿$A_2C与桌面成30^{\circ}$角,则点$A翻滚到A_2$时,共走过的路径长为( )

A.$10\pi\ cm$
B.$3.5\pi\ cm$
C.$4.5\pi\ cm$
D.$2.5\pi\ cm$

答案： B 解析:整条路径分两部分,从A到$A_1$是以BA长为半径,绕B点旋转$90°$;从$A_1$到$A_2$是以$CA_1$长为半径,绕C点旋转$60°$.总路径长为$\frac{90×\pi×5}{180}+\frac{60×\pi×3}{180}=3.5\pi\ (cm)$.

8. 在半径为 1 的圆中,长度等于$\sqrt{2}$的弦所对的圆心角是______度.

答案： 90

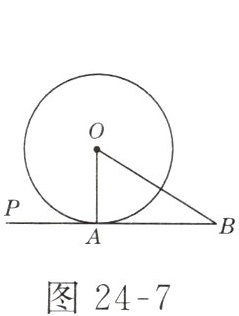
9. 如图 24-7 所示,$PB为\odot O$的切线,$A$为切点,$OB = 2\ cm$,$\angle B = 30^{\circ}$,则$AB = $______.

答案： $\sqrt{3}\ cm$ 解析:因为AB是$\odot O$的切线,所以$OA\perp AB$.又因为$\angle B=30°$,所以$OA=\frac{1}{2}OB=1\ cm$.在$Rt\triangle AOB$中,由勾股定理得$AB=\sqrt{2^2-1^2}=\sqrt{3}\ (cm)$.

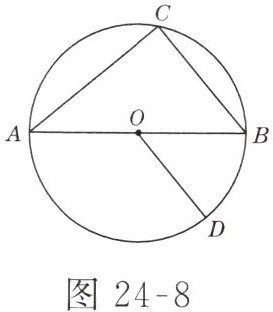
10. 如图 24-8 所示,$AB是\odot O$的直径,点$D在\odot O$上,$\angle AOD = 130^{\circ}$,$BC // OD交\odot O于点C$,则$\angle A = $______.

答案： $40°$ 解析:$\angle BOD=180°-130°=50°$,由$BC// OD$得$\angle B=\angle BOD=50°$.由AB是$\odot O$的直径可得$\angle ACB=90°$,所以$\angle A=90°-\angle B=90°-50°=40°$.

11. 在边长为 3 cm,4 cm,5 cm 的三角形白铁皮上剪下一个最大圆,则此圆的半径为______cm.

答案： 1 解析:由勾股定理的逆定理可得,边长为3 cm,4 cm,5 cm的三角形是直角三角形,其内切圆半径$r=\frac{3+4-5}{2}=1\ (cm)$.

12. 过圆上一点引两条互相垂直的弦,若圆心到两条弦的距离分别是 2 和 3,则这两条弦的长分别是______.

答案： 6,4 解析:因为两垂直弦的夹角为$90°$,所以两弦的非公共端点的连线是直径.由垂径定理和三角形中位线的性质定理,可得两弦长分别为6,4.

13. 如图 24-9 所示,在三角形$ABC$中,$\angle ACB = 90^{\circ}$,$\angle ABC = 30^{\circ}$,$BC = 6$,三角尺绕直角顶点$C$逆时针旋转,当点$A的对应点A'落在AB$边上时即停止转动,则点$B$转过的路径长为______.

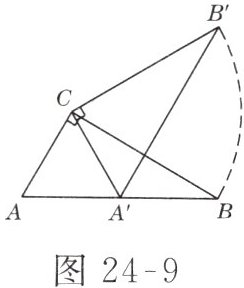
答案： $2\pi$ 解析:由题意得$\angle B'CB=60°$,$\overset{\frown}{BB'}=\frac{60\pi×6}{180}=2\pi$.