《2025年阳光课堂金牌练习册九年级数学上册人教版》

1. 有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( )

A.4 个
B.3 个
C.2 个
D.1 个

答案： B 解析:①③④正确.三点共线时过三点不能作圆,故②错误.

2. 如图 24-1 所示,$AB是\odot O$的直径,$AC是\odot O$的切线,$A$为切点,连接$BC交\odot O于点D$,连接$AD$.若$\angle ABC = 45^{\circ}$,则下列结论正确的是( )

A.$AD = \frac{1}{2}BC$
B.$AD = \frac{1}{2}AC$
C.$AC ＞ AB$
D.$AD ＞ DC$

答案： A 解析:因为AC是$\odot O$的切线,所以$BA\perp AC$.又因为$\angle B=45°$,所以$\angle C=45°$,所以$AB=AC$.又因为AB是直径,所以$AD\perp BC$.所以$BD=CD$(三线合一),所以$AD=\frac{1}{2}BC$.

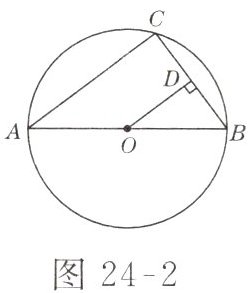
3. 如图 24-2 所示,$AB是\odot O$的直径,$C是\odot O$上的一点,若$AC = 8$,$AB = 10$,$OD \perp BC于点D$,则$BD$的长为( )

A.1.5
B.3
C.5
D.6

答案： B 解析:因为AB是直径,所以$\angle ACB=90°$.在$Rt\triangle ACB$中,$BC=\sqrt{10^2-8^2}=6$.因为$OD\perp BC$,所以$BD=\frac{1}{2}BC=3$(垂径定理).

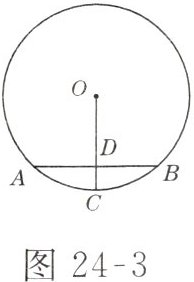
4. 如图 24-3 所示,$AB是\odot O$的弦,半径$OC \perp AB于点D$,且$AB = 6\ cm$,$OD = 4\ cm$,则$DC$的长为( )

A.5 cm
B.2.5 cm
C.2 cm
D.1 cm

答案： D 解析:连接AO(图略),由垂径定理知$AD=\frac{1}{2}AB=3\ cm$,所以在$Rt\triangle AOD$中,$AO=\sqrt{OD^2+AD^2}=\sqrt{4^2+3^2}=5\ (cm)$,所以$DC=OC-OD=OA-OD=5-4=1\ (cm)$.

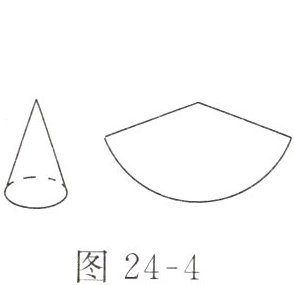
5. 如图 24-4 所示,圆锥侧面展开图的扇形面积为$65\pi\ cm^2$,扇形的弧长为$10\pi\ cm$,则圆锥的母线长是( )

A.5 cm
B.10 cm
C.12 cm
D.13 cm

答案： D 解析:圆锥的母线长$l$即为圆锥侧面展开图扇形的半径.由圆锥的侧面积公式,得$\frac{1}{2}×10\pi× l=65\pi$,所以$l=13\ cm$.