《2025年阳光课堂金牌练习册九年级数学上册人教版》

5. 已知点 $ P_1(a - 1, 1) $ 和 $ P_2(2, b - 1) $ 关于原点对称,则 $ a^b $ 的值为( )

A.$ 0 $
B.$ 1 $
C.$ -1 $
D.$ \pm 1 $

答案： B　解析:由题意得a−1+2=0,b−1+1=0,解得a=−1,b=0.所以aᵇ=(−1)⁰=1.

6. 将如图 23 - 5 所示的图案绕正六边形的中心旋转 $ n^{\circ} $时与原图案完全重合,那么 $ n $ 的最小值是( )

A.$ 60 $
B.$ 90 $
C.$ 120 $
D.$ 180 $

答案： C　解析:观察图形的组成特点可以发现图形外围的图案至少旋转120°后可以与原来的图案重合，内部的图案在旋转120°后也和原来的图案重合，故选C.

7. 下列说法正确的是( )

A.中心对称的两个图形一定是全等形
B.中心对称图形是旋转 $ 90^{\circ} $后能与自身重合的图形
C.两个形状、大小完全相同的图形一定中心对称
D.中心对称图形一定是轴对称图形

答案： A

8. 若 $ \triangle ABC $ 绕点 $ A $ 旋转能与 $ \triangle ADE $ 重合,其中 $ AB $ 与 $ AD $ 重合,$ AC $ 与 $ AE $ 重合. 若 $ \angle EAD = 120^{\circ} $,则 $ \angle CAB = $______；若 $ \angle CAE = 35^{\circ} $,则 $ \angle BAD = $______.

答案： 120°　35°　解析:由能互相重合的边得到对应边,从而确定对应角是解题关键,题中AB与AD重合,AC与AE重合,∠EAD与∠CAB是对应角,∠CAE与∠BAD是旋转角.

9. 在平面直角坐标系中,已知点 $ P_0 $ 的坐标为 $ (1, 0) $,将点 $ P_0 $ 绕原点 $ O $ 逆时针旋转 $ 60^{\circ} $得点 $ P_1 $,延长 $ OP_1 $ 到点 $ P_2 $,

使

$ OP_2 = 2OP_1 $,再将点 $ P_2 $ 绕原点 $ O $ 逆时针旋转 $ 60^{\circ} $得点 $ P_3 $,则点 $ P_3 $ 的坐标是______.

答案： (−1,$\sqrt{3}$)　解析:画图确定点P₃的位置，过该点作x轴、y轴的垂线段，得到直角三角形，可求出点P₃的坐标.解答此题结合图形比较简便.

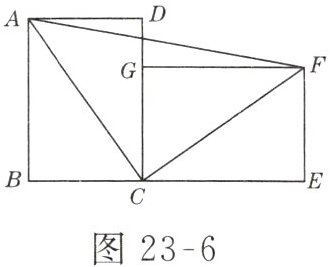
10. 如图 23 - 6 所示,用两块完全相同的矩形拼成“L”形,则 $ \angle ACF $ 的大小是______,$ \triangle ACF $ 的形状是______.

答案： 90°　等腰直角三角形　解析:矩形FGCE可以看作是由矩形ABCD绕点C顺时针旋转90°得到的,则∠ACF=90°,AC=FC,所以△ACF是等腰直角三角形.

11. 已知点 $ P(a^2 - 1, a^2 - 2a + 5) $ 在 $ y $ 轴上,则点 $ P $ 关于原点 $ O $ 对称的点的坐标为______.

答案： (0,−8)或(0,−4)　解析:因为点P(a²−1,a²−2a+5)在y轴上,所以a²−1=0,所以a=1或a=−1.当a=1时,a²−2a+5=4,当a=−1时,a²−2a+5=8,所以点P的坐标为(0,8)或(0,4),所以点P关于原点O对称的点的坐标为(0，−8)或(0,−4).

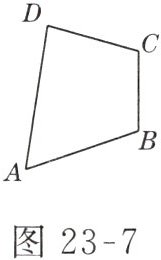
12. (12 分)如图 23 - 7 所示,画出四边形 $ ABCD $ 绕点 $ A $ 逆时针旋转 $ 90^{\circ} $ 后的图形.

答案：
解:如图PC−23−1所示,