《2025年练习与测试六年级数学上册苏教版》

(1)一个长方体饼干盒,长12厘米,宽8厘米,高14厘米。如果围着它贴一圈商标纸(上下面不贴,其余四面贴满),计算商标纸的面积至少是多少平方厘米,列式是( )。

A.12×8×2+12×14×2
B.12×14×2+8×14×2
C.12×8×2+8×14×2

答案： B

(2)市民中心新建一个长方体游泳池,长80米,宽25米,深3米。现要在游泳池的侧面和底面都贴上瓷砖,计算贴瓷砖的面积一共是多少平方米,列式是( )。

A.80×25×2+25×3×2+80×3
B.80×3×2+80×25×2+25×3
C.(80×25+80×3+25×3)×2-80×25

答案： C

2. 水产品市场存放活鱼的长方体铁皮水箱(无盖)长1.1米,宽0.8米,高0.5米。做这个水箱至少要用铁皮多少平方米？

答案： 答题卡：
水箱无盖，所以表面积由底面和四个侧面组成。
底面面积：
$1.1 × 0.8 = 0.88$（平方米）。
两个长×高的侧面面积：
$2 × (1.1 × 0.5) = 1.1$（平方米）。
两个宽×高的侧面面积：
$2 × (0.8 × 0.5) = 0.8$（平方米）。
总面积：
$0.88 + 1.1 + 0.8 = 2.78$（平方米）。
答：做这个水箱至少要用铁皮2.78平方米。

3. 如图,在一个棱长3分米的正方体的一个顶点处挖去一个棱长1分米的小正方体。求剩下部分的表面积。

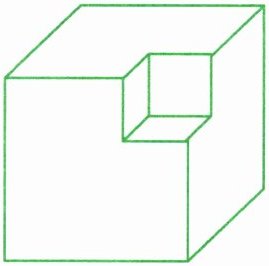
答案： 原正方体棱长为3分米，根据正方体表面积公式$S = 6a^2$（$a$为棱长），原正方体表面积$S=6×3^2 = 6×9 = 54$平方分米。
在顶点处挖去一个小正方体后，减少了小正方体$3$个面的面积，同时又增加了小正方体$3$个面的面积，所以剩下部分的表面积与原正方体表面积相等，为$54$平方分米。
答：剩下部分的表面积是54平方分米。