《2025年配套练习与检测四年级数学上册人教版》

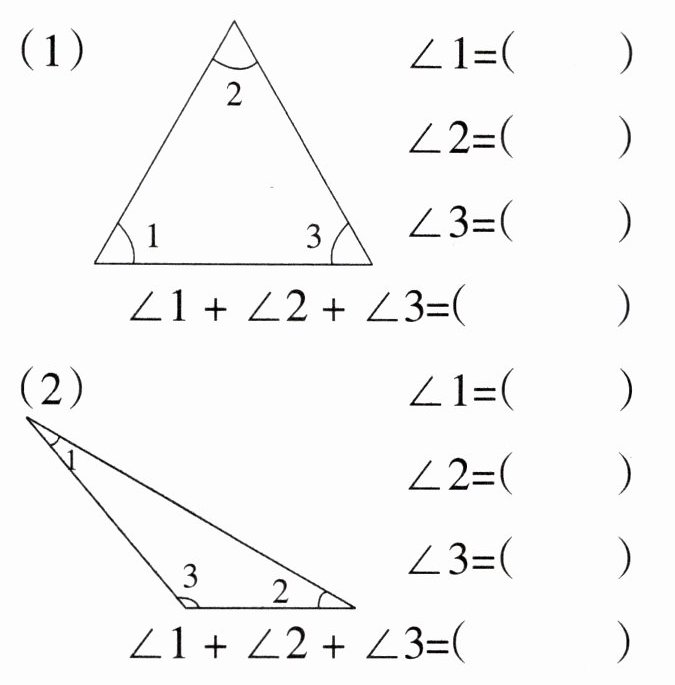
3. 量出下面每个三角形三个角的度数,并计算三个角的和。你有什么发现？

我发现：任意三角形的内角和都是180°

答案：
(1)60° 60 60° 180°
(2)20° 30° 130° 180°
我发现：任意三角形的内角和都是180°

4. 量出下面各角的度数。你有什么发现？

我发现：对顶角度数相等（答案不唯一,合理即可）

答案： 135° 45° 135° 45°
我发现：对顶角度数相等（答案不唯一,合理即可）

5. 先量出每个角的度数,再填一填。
    
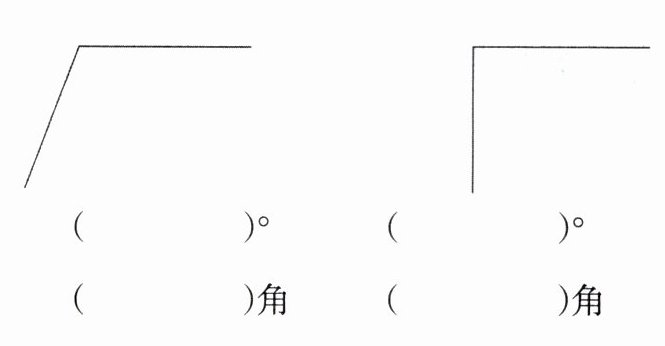
120 钝 25 锐 110 钝 90 直

答案： 120 钝 25 锐 110 钝 90 直

6. 已知∠1= 35°,求∠2、∠3和∠5各是多少度？

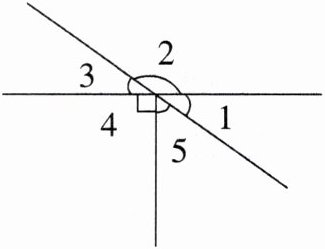
答案： ∠2=145° ∠3=35° ∠5=55°

7. 下图中∠1= ∠2= ∠3,∠1+∠2+∠3= 90°。

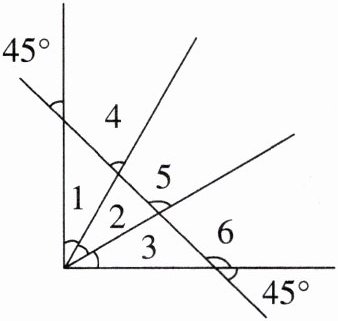
(1)∠1= (30°),∠2= (30°),∠3= (30°),∠6= (135°)。
(2)图中有(10)条线段,有(1)条直线。
(3)图中所有的角中,有(13)个锐角,(1)个直角,(8)个钝角。
(4)用三角尺画一个与∠3相等的角,用量角器画一个与∠6相等的角。

答案： 1. （1）
因为$\angle1 = \angle2=\angle3$，且$\angle1+\angle2+\angle3 = 90^{\circ}$，所以$\angle1=\angle2=\angle3=\frac{90^{\circ}}{3}=30^{\circ}$。
又因为$\angle3 + \angle6=180^{\circ}-45^{\circ}=135^{\circ}$，$\angle3 = 30^{\circ}$，所以$\angle6=135^{\circ}-\angle3=135^{\circ}-30^{\circ}=105^{\circ}$。
故$\angle1=(30^{\circ})$，$\angle2=(30^{\circ})$，$\angle3=(30^{\circ})$，$\angle6=(105^{\circ})$。
2. （2）
线段是指直线上两点间的有限部分，图中的线段有：$3$条（可以通过数图中两点之间的部分得到）。
直线没有端点，向两方无限延伸，图中的直线有：$2$条（根据直线的定义判断）。
故图中有$(3)$条线段，有$(2)$条直线。
3. （3）
锐角是大于$0^{\circ}$而小于$90^{\circ}$的角，$\angle1$、$\angle2$、$\angle3$、$\angle4$、$\angle5$都是锐角，共$5$个。
直角是等于$90^{\circ}$的角，图中有$2$个直角（根据直角的定义判断）。
钝角是大于$90^{\circ}$小于$180^{\circ}$的角，$\angle6$是钝角，有$1$个。
故图中所有的角中，有$(5)$个锐角，$(2)$个直角，$(1)$个钝角。
4. （4）
用三角尺画与$\angle3$（$30^{\circ}$）相等的角：
步骤：先画一条射线，将三角尺$30^{\circ}$角的顶点与射线的端点重合，一条边与射线重合，在三角尺$30^{\circ}$角的另一条边上点一个点，然后以射线的端点为端点，通过刚才点的点，再画一条射线，这样就画出了$30^{\circ}$的角。
用量角器画与$\angle6$（$105^{\circ}$）相等的角：
步骤：先画一条射线，将量角器的中心与射线的端点重合，$0^{\circ}$刻度线与射线重合，在量角器$105^{\circ}$刻度线的地方点一个点，最后以射线的端点为端点，通过刚才点的点，再画一条射线，这样就画出了$105^{\circ}$的角。