《2025年天天练口算六年级数学上册人教版》

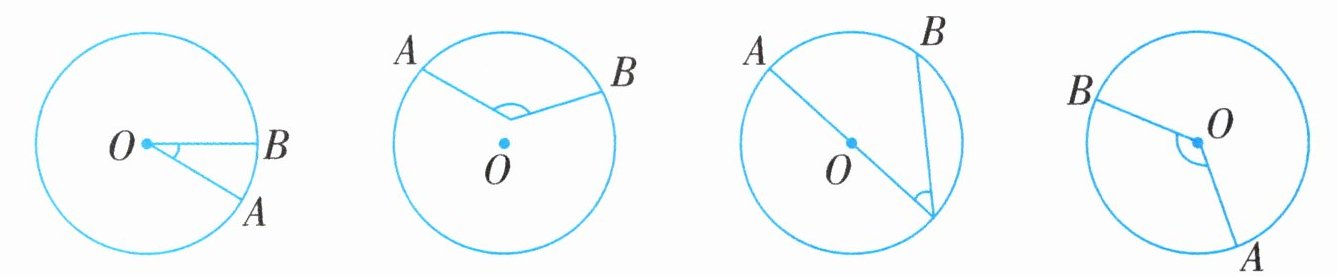
哪些是圆心角,是的在( )里打“√”

()
(√)
()
(√)

答案： 本题可根据圆心角的定义来判断所给角是否为圆心角。
圆心角的定义为：顶点在圆心的角叫做圆心角。
据此逐一分析所给的角：
第一个角：该角的顶点在圆上，不在圆心，所以它不是圆心角。
第二个角：该角的顶点在圆心，所以它是圆心角。
第三个角：该角的顶点在圆上，不在圆心，所以它不是圆心角。
第四个角：该角的顶点在圆心，所以它是圆心角。
综上，答案依次为：( )；(√)；( )；(√)。

大圆和小圆半径比是(2:1);
大圆和小圆直径比是(2:1);
大圆和小圆周长比是(2:1);
大圆和小圆面积比是(4:1)。

答案： 解析：本题主要考查圆的半径、直径、周长和面积之间的关系以及比的计算。需要根据圆的性质分别求出大圆和小圆的直径、周长和面积，再计算它们的比值。
大圆半径$R = 10$cm，小圆半径$r = 5$cm，则大圆和小圆半径比是$10:5 = 2:1$。
圆的直径$d = 2r$（$r$为半径），那么大圆直径$D = 2×10 = 20$（cm），小圆直径$d = 2×5 = 10$（cm），所以大圆和小圆直径比是$20:10 = 2:1$。
圆的周长$C = 2\pi r=\pi d$（$r$为半径，$d$为直径），那么大圆周长$C_{大}=2\pi×10 = 20\pi$（cm），小圆周长$C_{小}=2\pi×5 = 10\pi$（cm），所以大圆和小圆周长比是$20\pi:10\pi = 2:1$。
圆的面积$S=\pi r^{2}$（$r$为半径），那么大圆面积$S_{大}=\pi×10^{2}=100\pi$（$cm^2$），小圆面积$S_{小}=\pi×5^{2} = 25\pi$（$cm^2$），所以大圆和小圆面积比是$100\pi:25\pi = 4:1$。
答案：$2:1$；$2:1$；$2:1$；$4:1$。

$\frac {5}{6}+x= 3$
$x=$$\frac{13}{6}$
$\frac {1}{12}+x= \frac {3}{4}$
$x=$$\frac{2}{3}$
$\frac {1}{3}-x= \frac {2}{9}$
$x=$$\frac{1}{9}$
$x-\frac {1}{4}= \frac {1}{4}$
$x=$$\frac{1}{2}$
$\frac {5}{12}-x= \frac {1}{12}$
$x=$$\frac{1}{3}$
$\frac {2}{3}+x= 1$
$x=$$\frac{1}{3}$
$2x-\frac {3}{4}= \frac {1}{4}$
$x=$$\frac{1}{2}$
$\frac {3}{5}+x= 2$
$x=$$\frac{7}{5}$

答案： 解析：这些题目都是一元一次方程的求解问题，需要通过移项和通分等方法求解未知数。
答案：
1.
$\frac{5}{6} + x = 3$
$x = 3 - \frac{5}{6}$
$x = \frac{18}{6} - \frac{5}{6}$
$x = \frac{13}{6}$
2.
$\frac{1}{12} + x = \frac{3}{4}$
$x = \frac{3}{4} - \frac{1}{12}$
$x = \frac{9}{12} - \frac{1}{12}$
$x = \frac{8}{12}$
$x = \frac{2}{3}$
3.
$\frac{1}{3} - x = \frac{2}{9}$
$x = \frac{1}{3} - \frac{2}{9}$
$x = \frac{3}{9} - \frac{2}{9}$
$x = \frac{1}{9}$
4.
$x - \frac{1}{4} = \frac{1}{4}$
$x = \frac{1}{4} + \frac{1}{4}$
$x = \frac{2}{4}$
$x = \frac{1}{2}$
5.
$\frac{5}{12} - x = \frac{1}{12}$
$x = \frac{5}{12} - \frac{1}{12}$
$x = \frac{4}{12}$
$x = \frac{1}{3}$
6.
$\frac{2}{3} + x = 1$
$x = 1 - \frac{2}{3}$
$x = \frac{3}{3} - \frac{2}{3}$
$x = \frac{1}{3}$
7.
$2x - \frac{3}{4} = \frac{1}{4}$
$2x = \frac{1}{4} + \frac{3}{4}$
$2x = 1$
$x = \frac{1}{2}$
8.
$\frac{3}{5} + x = 2$
$x = 2 - \frac{3}{5}$
$x = \frac{10}{5} - \frac{3}{5}$
$x = \frac{7}{5}$