1. 填一填。
(1)过一点可以画出( )条射线,过两点可以画出( )条直线。
(2)线段有( )个端点,射线有( )个端点,直线有( )个端点。
(3)数一数,右图中一共有( )条直线,( )条射线。
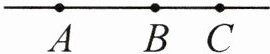
(1)过一点可以画出( )条射线,过两点可以画出( )条直线。
(2)线段有( )个端点,射线有( )个端点,直线有( )个端点。
(3)数一数,右图中一共有( )条直线,( )条射线。
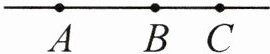
答案:
1.
(1)无数 1
(2)2 1 0
(3)1 6
解析
(1)从一个点出发,可以向任意方向画射线,所以可以画出无数条射线,过两点只能画出1条直线。
(2)线段有2个端点,射线有1个端点,直线没有端点,也就是0个端点。
(3)观察发现图中有1条直线。从点A出发有2条射线,从点B出发有2条射线,从点C 出发有2条射线,所以一共有2+2+2=6 (条)射线。
(1)无数 1
(2)2 1 0
(3)1 6
解析
(1)从一个点出发,可以向任意方向画射线,所以可以画出无数条射线,过两点只能画出1条直线。
(2)线段有2个端点,射线有1个端点,直线没有端点,也就是0个端点。
(3)观察发现图中有1条直线。从点A出发有2条射线,从点B出发有2条射线,从点C 出发有2条射线,所以一共有2+2+2=6 (条)射线。
2. 选一选。(将正确答案的序号填在括号里)
(1)“有始有终”可以用来形容( )。
A.直线 B.射线 C.线段
(2)如图,点 1、2、3、4、5 在同一条直线上,用探照灯从点 2 射出一条光线,当光线穿过点 3 后,一定不能穿过点( )。
A.1 B.4 C.5
(1)“有始有终”可以用来形容( )。
A.直线 B.射线 C.线段
(2)如图,点 1、2、3、4、5 在同一条直线上,用探照灯从点 2 射出一条光线,当光线穿过点 3 后,一定不能穿过点( )。

A.1 B.4 C.5
答案:
2.
(1)C
(2)A
解析
(1)“有始有终”也就是有起始的端点和最终的端点,有2个端点是线段,本题选C。
(2)可以近似的将探照灯光当作射线,这个射线的端点是点2,已知光线穿过点3,那么可以连接点2、点3,点1在点2向外延伸的线上,所以一定不能穿过点1,本题选A。
(1)C
(2)A
解析
(1)“有始有终”也就是有起始的端点和最终的端点,有2个端点是线段,本题选C。
(2)可以近似的将探照灯光当作射线,这个射线的端点是点2,已知光线穿过点3,那么可以连接点2、点3,点1在点2向外延伸的线上,所以一定不能穿过点1,本题选A。
3. 在框中按要求画图。
(1)画长 6 厘米的线段 AB。
(2)画射线 CD。
(3)利用圆规在射线 CD 上画线段 CE,使 CE= AB。

(1)画长 6 厘米的线段 AB。
(2)画射线 CD。
(3)利用圆规在射线 CD 上画线段 CE,使 CE= AB。

答案:
3

解析
(1)先任意画点A,用直尺的0刻度线对准这个端点,在直尺6厘米刻度线的地方点一个点B,连接这两个点即可。
(2)先任意画点C,然后向任意方向画一条射线CD即可。
(3)先将有针尖的脚放在点A上,另一只脚放在点B上,然后保持有针尖的脚与另一只脚之间距离不变,将有针尖的脚放在点C上,旋转手柄画出线与射线CD相交于点E。
3

解析
(1)先任意画点A,用直尺的0刻度线对准这个端点,在直尺6厘米刻度线的地方点一个点B,连接这两个点即可。
(2)先任意画点C,然后向任意方向画一条射线CD即可。
(3)先将有针尖的脚放在点A上,另一只脚放在点B上,然后保持有针尖的脚与另一只脚之间距离不变,将有针尖的脚放在点C上,旋转手柄画出线与射线CD相交于点E。
4. 探究活动:数线段。(填一填)
|图形|线段上的点数|线段的条数|
||2|1|
||3|2+1= 3|
 ||4| |
||4| |
||5| |
|图形|线段上的点数|线段的条数|
||2|1|
||3|2+1= 3|
 ||4| |
||4| |||5| |
答案:
4.3+2+1=6 4+3+2+1=10
解析数线段时可以先固定一个最左边的端点,数出这个端点与右边的端点能组成多少条线段,然后再从左到右的依次固定一个端点,数出还能组成多少条线条,直至固定的端点为最右边的端点,再将数出来的线段数量相加即可。第3个图形,先固定点A,那么可以组成AB、AC、AD共3条线段;然后固定点B,那么可以组成BC、BD共2条线段;再固定点C,那么可以组成CD这1条线段;最后固定点D,点D右边再无端点,所以无法组成线段。因此,第3个图形中线段的条数一共是3+2+1=6(条)。同理,数得第4个图形中线段的条数是4+3+2+1=10(条)。
解析数线段时可以先固定一个最左边的端点,数出这个端点与右边的端点能组成多少条线段,然后再从左到右的依次固定一个端点,数出还能组成多少条线条,直至固定的端点为最右边的端点,再将数出来的线段数量相加即可。第3个图形,先固定点A,那么可以组成AB、AC、AD共3条线段;然后固定点B,那么可以组成BC、BD共2条线段;再固定点C,那么可以组成CD这1条线段;最后固定点D,点D右边再无端点,所以无法组成线段。因此,第3个图形中线段的条数一共是3+2+1=6(条)。同理,数得第4个图形中线段的条数是4+3+2+1=10(条)。
查看更多完整答案,请扫码查看


