《2025年练习部分七年级数学上册沪教版五四制》

4. 用含$a$、$b$的整式填空：
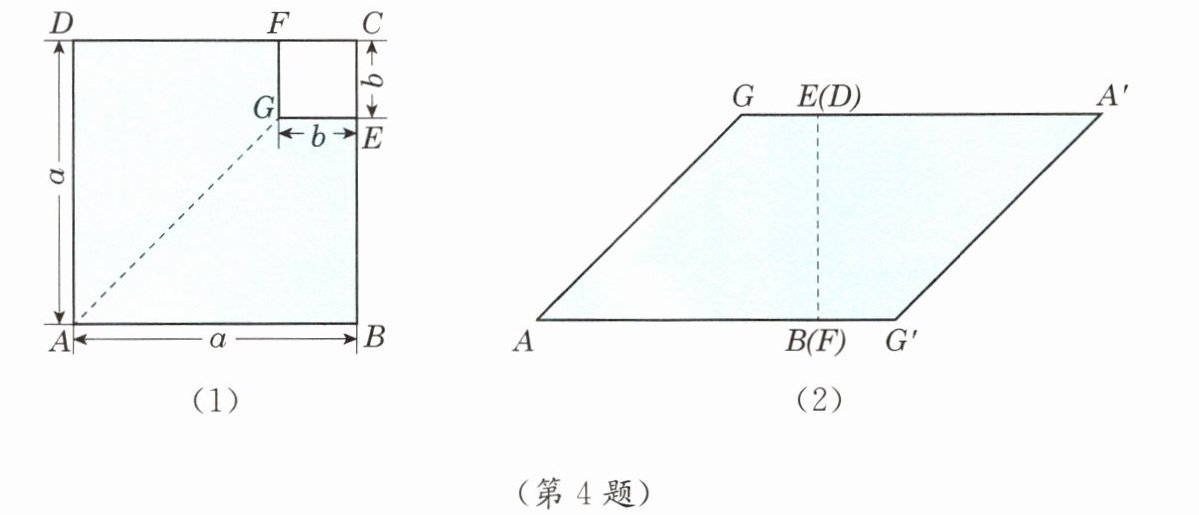
如图(1),正方形$ABCD的边长为a$,正方形$ECFG的边长为b$,其中点$E$、$F分别在边BC$、$CD$上。一方面,涂色部分的面积等于两个正方形的面积之差,为$\underline{a²-b²}$；另一方面,连接$AG$,可将涂色部分分割成两个面积相等的四边形。将两个四边形拼成如图(2)所示的平行四边形$AGA'G'$。它的底边$AG'等于\underline{a+b}$,底边$AG'上的高等于\underline{a-b}$,则该平行四边形的面积为$\underline{(a+b)(a-b)}$。此时图(2)中的平行四边形的面积等于图(1)中涂色部分的面积,于是我们得到$\underline{(a+b)(a-b)} = \underline{a²-b²}$。

答案： 4. a²-b²; a+b; a-b; (a+b)(a-b); (a+b)(a-b); a²-b².

1. 填空题：
(1) $(y + 2)^2 = $$y^{2}+4y+4$；
(2) $(3 - 2a)^2 = $$9-12a+4a^{2}$；
(3) $\left(\dfrac{1}{2} - 3x\right)^2 = $$\frac{1}{4}-3x+9x^{2}$；
(4) $\left(\dfrac{1}{3}a + 3b\right)^2 = $$\frac{1}{9}a^{2}+2ab+9b^{2}$；
(5) $(x - y)(y - x) = $$-x^{2}+2xy-y^{2}$；
(6) $(-x - y)(x + y) = $$-x^{2}-2xy-y^{2}$；
(7) $(a + b)^2 + (a - b)^2 = $$2a^{2}+2b^{2}$；
(8) $(a + b)^2 - (a - b)^2 = $$4ab$。

答案： （1）$y^{2}+4y+4$.（2）$9-12a+4a^{2}$.（3）$\frac{1}{4}-3x+9x^{2}$.（4）$\frac{1}{9}a^{2}+2ab+9b^{2}$.（5）$-x^{2}+2xy-y^{2}$.（6）$-x^{2}-2xy-y^{2}$.（7）$2a^{2}+2b^{2}$.（8）$4ab$.