1. 填空题:
(1) $(a + 2) \cdot (a + 3) = $
(2) $(a^{2} + 2) \cdot (a^{2} - 3) = $
(3) $(y^{3} - 2) \cdot (y^{3} - 3) = $
(4) $(ab - 2) \cdot (ab + 3) = $
(1) $(a + 2) \cdot (a + 3) = $
$a^{2}+5a+6$
;(2) $(a^{2} + 2) \cdot (a^{2} - 3) = $
$a^{4}-a^{2}-6$
;(3) $(y^{3} - 2) \cdot (y^{3} - 3) = $
$y^{6}-5y^{3}+6$
;(4) $(ab - 2) \cdot (ab + 3) = $
$a^{2}b^{2}+ab-6$
.
答案:
(1)$a^{2}+5a+6$.(2)$a^{4}-a^{2}-6$.(3)$y^{6}-5y^{3}+6$.(4)$a^{2}b^{2}+ab-6$.
2. 如图,长方形 $ABCD$ 的一组邻边的长分别为
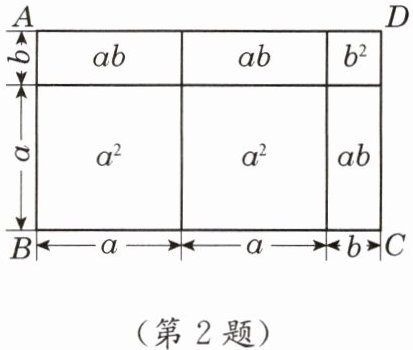
$2a+b$
与$a+b$
. 一方面,由长方形的面积公式,可知长方形 $ABCD$ 的面积可以表示为$(2a+b)\bullet (a+b)$
;另一方面,长方形 $ABCD$ 被分成 6 个小长方形,它们的面积之和为$2a^{2}+3ab+b^{2}$
. 于是我们得到$(2a+b)\bullet (a+b)$
$=$$2a^{2}+3ab+b^{2}$
. (用含 $a$、$b$ 的整式表示)
答案:
$2a+b$;$a+b$;$(2a+b)\bullet (a+b)$;$2a^{2}+3ab+b^{2}$;$(2a+b)\bullet (a+b)=2a^{2}+3ab+b^{2}$.
3. 计算:
(1) $(1 - 4x) \cdot \left(\frac{1}{2} + 4x^{2}\right)$;
(2) $(x^{2} + 5y) \cdot (-y^{2} + 6x)$;
(3) $(2x + 3y) \cdot \left(\frac{1}{2}x - \frac{1}{3}y\right)$;
(4) $(a^{2} + 2ab + 4b^{2}) \cdot (a - 2b)$;
(5) $(3x + 2y) \cdot (2x + 3y) - 2(x - 3y) \cdot (3x + 4y)$.
(1) $(1 - 4x) \cdot \left(\frac{1}{2} + 4x^{2}\right)$;
(2) $(x^{2} + 5y) \cdot (-y^{2} + 6x)$;
(3) $(2x + 3y) \cdot \left(\frac{1}{2}x - \frac{1}{3}y\right)$;
(4) $(a^{2} + 2ab + 4b^{2}) \cdot (a - 2b)$;
(5) $(3x + 2y) \cdot (2x + 3y) - 2(x - 3y) \cdot (3x + 4y)$.
答案:
(1)$\frac{1}{2}+4x^{2}-2x-16x^{3}$.(2)$-x^{2}y^{2}+6x^{3}-5y^{3}+30xy$.(3)$x^{2}+\frac{5}{6}xy-y^{2}$.(4)$a^{3}-8b^{3}$.(5)$23xy+30y^{2}$.
查看更多完整答案,请扫码查看


