第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
5. 填表.
|多项式|多项式的项|常数项|最高次项|多项式的次数|
|$-2x + 8$|||||
|$x^{2}-5x^{4}+3$|||||
|$x^{2}y+xy - y^{3}-1$|||||
|多项式|多项式的项|常数项|最高次项|多项式的次数|
|$-2x + 8$|||||
|$x^{2}-5x^{4}+3$|||||
|$x^{2}y+xy - y^{3}-1$|||||
答案:
|多项式|多项式的项|常数项|最高次项|多项式的次数|
|-2x + 8|$-2x,8$|8|$-2x$|1|
|$x^{2}-5x^{4}+3$|$x^{2},-5x^{4},3$|3|$-5x^{4}$|4|
|$x^{2}y+xy - y^{3}-1$|$x^{2}y,xy,-y^{3},-1$|$-1$|$x^{2}y$和$-y^{3}$|3|
|-2x + 8|$-2x,8$|8|$-2x$|1|
|$x^{2}-5x^{4}+3$|$x^{2},-5x^{4},3$|3|$-5x^{4}$|4|
|$x^{2}y+xy - y^{3}-1$|$x^{2}y,xy,-y^{3},-1$|$-1$|$x^{2}y$和$-y^{3}$|3|
6. 多项式 $\frac{5x^{2}-2}{7}$ 的常数项是______.
答案:
$-\frac{2}{7}$
7. 把下列代数式分别填在相应的括号内.
$2 - ab$,$-3a^{2}+\frac{1}{2}$,$-\frac{ab^{2}}{4}$,$-4\frac{1}{2}$,$-\frac{1}{2}a$,$-2a^{2}+3a + 1$,$\frac{a^{2}+b^{2}}{4}$,$\pi a + 1$.
(1)单项式:…{$$}.
(2)多项式:…{$$}.
$2 - ab$,$-3a^{2}+\frac{1}{2}$,$-\frac{ab^{2}}{4}$,$-4\frac{1}{2}$,$-\frac{1}{2}a$,$-2a^{2}+3a + 1$,$\frac{a^{2}+b^{2}}{4}$,$\pi a + 1$.
(1)单项式:…{$$}.
(2)多项式:…{$$}.
答案:
(1)单项式:$\{ -\frac{ab^{2}}{4},-4\frac{1}{2},-\frac{1}{2}a,\cdots \} $;(2)多项式:$\{ 2-ab,-3a^{2}+\frac{1}{2},-2a^{2}+3a+1,\frac{a^{2}+b^{2}}{4},\pi a+1,\cdots \} $.
8. 若多项式 $3x^{m}y^{2}+(n + 3)x^{2}y+2x + 1$ 是关于 $x$,$y$ 的四次三项式,则 $n^{m}$ 的值为______.
答案:
9
9. 已知多项式 $x^{\vert m\vert}-(m + 2)x + 12$ 是关于 $x$ 的二次二项式,求 $m$ 的值.
答案:
解:因为多项式$x^{|m|}-(m+2)x+12$是关于x的二次二项式,所以$|m|=2$,且$m+2=0$,解得$m=-2$,即m的值是-2.
10. 观察下面的点阵图和相应的等式,探究其中的规律.
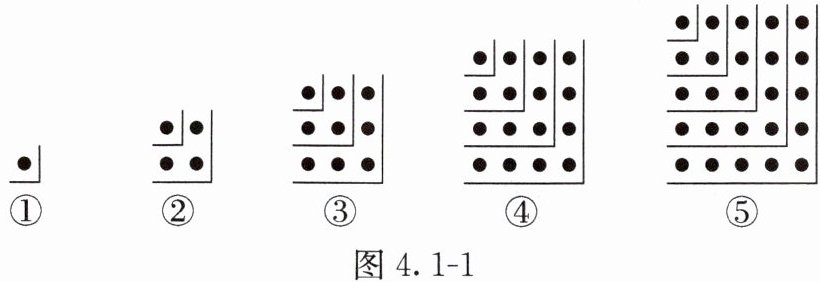
(1)在④后面的横线上写出相应的等式:
①$1 = 1^{2}$;②$1 + 3 = 2^{2}$;③$1 + 3 + 5 = 3^{2}$;④______.
(2)试用含有 $n$ 的式子表示这一规律:$1 + 3 + 5 + 7 + 9 + …+$______= $n^{2}$($n$ 为正整数);
(3)请根据上面的规律计算:$101 + 103 + 105 + 107 + …+197 + 199$.

(1)在④后面的横线上写出相应的等式:
①$1 = 1^{2}$;②$1 + 3 = 2^{2}$;③$1 + 3 + 5 = 3^{2}$;④______.
(2)试用含有 $n$ 的式子表示这一规律:$1 + 3 + 5 + 7 + 9 + …+$______= $n^{2}$($n$ 为正整数);
(3)请根据上面的规律计算:$101 + 103 + 105 + 107 + …+197 + 199$.
答案:
(1)$1+3+5+7=4^{2}$;(2)$2n-1$ $n^{2}$;(3)(解法不唯一)$101+103+105+107+\cdots +197+199=(1+3+\cdots +199)-(1+3+\cdots +99)=100^{2}-50^{2}=7500$.
查看更多完整答案,请扫码查看


