《2025年能力培养与测试七年级数学上册人教版》

6. 计算：
(1) $3^{3}×(-\frac{1}{3})-2^{4}÷(-\frac{1}{2})$；
(2) $4-(-2)^{3}-3^{2}÷(-1)+0×(-5)^{2}$；
(3) $1\frac{1}{3}×[1-(-4)^{2}]-(-2)^{3}÷\frac{4}{5}$；
(4) $-2^{4}-8×(-\frac{1}{4})^{2}+\frac{3}{4}$.

答案： 解:
(1)原式=23.　　　
(2)原式=21.　
(3)原式=−10.　　　
(4)原式=−$\frac{63}{4}$.

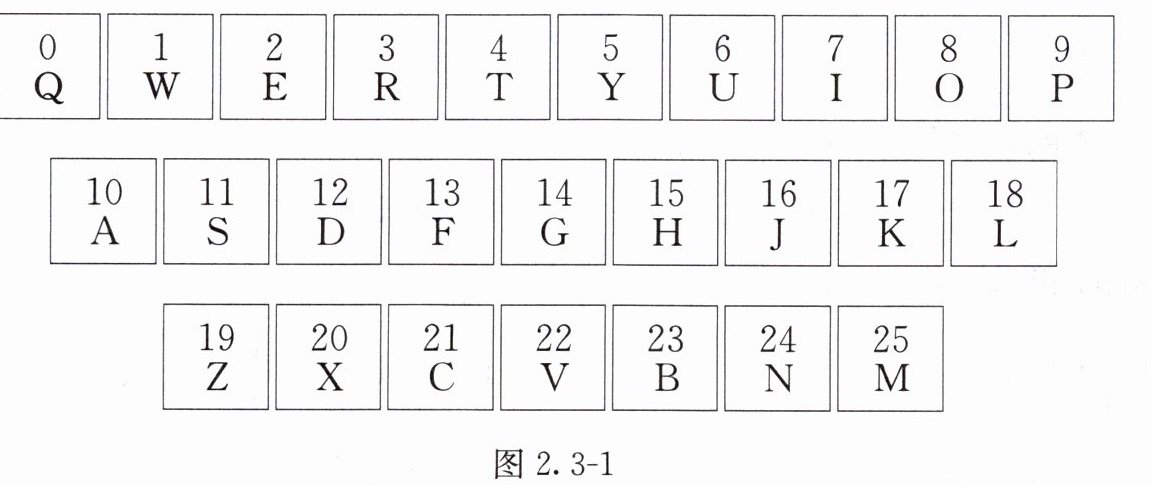
7. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密). 已知有一种键盘密码,每个字母与所在按键的数字序号对应(见图2.3 - 1),如字母Q与数字序号0对应. 当明文中的字母对应的序号为$a$时,将$(a + 7)$除以26后所得的余数作为密文中的字母对应的序号,例如明文“X”对应密文“W”. 按上述规定,将密文“TKGDFY”解密成明文后是( ).


A.DAISHU
B.TUXING
C.BAIYUN
D.SHUXUE

答案： C

8. 按图2.3 - 2所示的程序计算,若开始输入的$n的值为-2$,则最后输出的结果是______.

答案： 73

9. 求$1 + 2 + 2^{2} + 2^{3} + … + 2^{2024}$的值.
令$S = 1 + 2 + 2^{2} + 2^{3} + … + 2^{2024}$,则$2S = 2 + 2^{2} + 2^{3} + 2^{4} + … + 2^{2025}$,因此$2S - S = 2^{2025} - 1$,$S = 2^{2025} - 1$. 我们把这种求和方法叫错位相减法.
仿照上述的思路方法,计算：$1 + 5 + 5^{2} + 5^{3} + … + 5^{2024} = $______.

答案： $\frac{5^{2025}-1}{4}$

10. 如图2.3 - 3,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的长方形,接着把其中一个面积为$\frac{1}{2}的长方形等分成两个面积为\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}的正方形等分成两个面积为\frac{1}{8}$的长方形……如此进行下去.
(1) 试利用图形揭示规律,计算：
$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + … + \frac{1}{2^{n}} = $______,并使用代数方法说明你的结论正确(提示：参考第9题)；
(2) 请你再设计一个能求出$\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + … + \frac{1}{2^{n}}$的值的几何图形.

答案：
解:
(1)$1-\frac{1}{2^{n}}$ 说明如下:令$S=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\cdots+\frac{1}{2^{n}}$，①则$2S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\cdots+\frac{1}{2^{n-1}}$，②用②式减去①式，得$S=1-\frac{1}{2^{n}}$.　　
(2)如图:(答案不唯一)