《2025年初中同步测控优化设计九年级数学全一册人教版》

4. 现有四张完全相同的卡片,上面分别标有数字 $-1$,$-2$,$3$,$4$。把卡片背面朝上洗匀,然后从中随机抽取两张,则这两张卡片上的数字之积为负数的概率是2/3。

答案： 2/3

5. 现有四张正面分别标有数字 $-1$,$1$,$2$,$3$ 的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为 $m$,$n$,则点 $P(m,n)$ 在第二象限的概率为$\frac{3}{16}$。

答案： $\frac{3}{16}$（或写成$0.1875$，但题目中概率一般以分数形式表示，故答案为$\frac{3}{16}$对应的填空答案，若为选择则根据选项选择）

6. 一张圆桌旁有四个座位,$A$ 先坐在如图所示的座位上,$B$,$C$,$D$ 三人随机坐到其他三个座位上,求 $A$ 与 $B$ 不相邻而坐的概率。

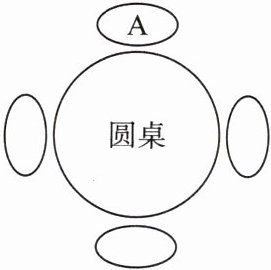
答案： $\frac{1}{3}$

7. 一只不透明的袋子中装有 $2$ 个白球和 $1$ 个红球,这些球除颜色外都相同,搅匀后从中任意摸出 $1$ 个球(不放回),再从余下的 $2$ 个球中任意摸出 $1$ 个球。
(1)用列表法列出所有可能出现的结果；
(2)求两次摸到的球的颜色不同的概率。

答案： 答题卡：
(1) 设两个白球分别为$W_1$，$W_2$，红球为$R$。
列表法列出所有可能出现的结果：
$\begin{array}{c|c|c}第一次 & 第二次 & 结果 \\\hlineW_1 & W_2 & (W_1, W_2) \\W_1 & R & (W_1, R) \\W_2 & W_1 & (W_2, W_1) \\W_2 & R & (W_2, R) \\R & W_1 & (R, W_1) \\R & W_2 & (R, W_2) \\\end{array}$
(2) 两次摸到的球颜色不同的情况有：
$(W_1, R), (W_2, R), (R, W_1), (R, W_2)$，共4种。
总共有6种等可能的结果，所以两次摸到的球颜色不同的概率为：
$P = \frac{4}{6} = \frac{2}{3}$。

8. 小明和小刚玩摸纸牌游戏,如图,两组相同的纸牌,每组两张,纸面数字分别是 $2$ 和 $3$,将两组牌背面朝上,洗匀后从每组牌中各摸出一张,称为一次游戏。当两张牌牌面数字之和为奇数,小明得 $2$ 分,否则小刚得 $1$ 分,这个游戏对双方公平吗？请说明理由。

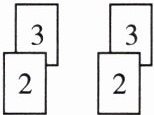
答案： 用列举法列出所有可能的结果：
设第一组牌的数字为$A$，第二组牌的数字为$B$，则所有可能的结果为：
$(A, B) = \{(2,2), (2,3), (3,2), (3,3)\}$，
计算两张牌牌面数字之和为奇数的概率：
和为奇数的组合有：$(2,3)$和$(3,2)$，共2种情况。
所有可能的情况有4种，所以和为奇数的概率为：
$P(和为奇数) = \frac{2}{4} = \frac{1}{2}$，
计算两张牌牌面数字之和为偶数的概率：
和为偶数的组合有：$(2,2)$和$(3,3)$，共2种情况。
所以和为偶数的概率为：
$P(和为偶数) = \frac{2}{4} = \frac{1}{2}$，
计算双方得分的期望值：
小明得分的期望值为：
$E(小明) = \frac{1}{2} × 2 = 1$，
小刚得分的期望值为：
$E(小刚) = \frac{1}{2} × 1 = 0.5$，
由于$E(小明) \neq E(小刚)$，所以这个游戏对双方不公平。

9. 小军与小玲共同发明了一种“字母棋”,进行比胜负的游戏。他们用四种字母做成 $10$ 枚棋子,其中 $A$ 棋 $1$ 枚,$B$ 棋 $2$ 枚,$C$ 棋 $3$ 枚,$D$ 棋 $4$ 枚。

“字母棋”的游戏规则为：①游戏时两人随机各摸一枚棋进行比赛称一轮比赛,先摸者摸出的棋不放回；②$A$ 棋胜 $B$ 棋,$C$ 棋；$B$ 棋胜 $C$ 棋,$D$ 棋；$C$ 棋胜 $D$ 棋；$D$ 棋胜 $A$ 棋；③相同棋子不分胜负。
(1)若小玲先摸,则小玲摸到 $C$ 棋的概率是多少？
(2)已知小玲先摸到了 $C$ 棋,小军在剩余的 $9$ 枚棋中随机摸一枚,问这一轮中小玲胜小军的概率是多少？
(3)已知小玲先摸一枚棋,小军在剩余的 $9$ 枚棋中随机摸一枚,问这一轮中小玲摸到哪种棋使她胜小军的概率最大？

答案：
(1)
总共有$10$枚棋子，其中$C$棋有$3$枚，根据概率公式$P(A)=\frac{m}{n}$（$n$是基本事件总数，$m$是事件$A$所包含的基本事件数），小玲摸到$C$棋的概率$P = \frac{3}{10}$。
(2)
小玲先摸到了$C$棋，此时剩余$9$枚棋，$C$棋胜$D$棋，$D$棋有$4$枚，所以这一轮中小玲胜小军的概率$P=\frac{4}{9}$。
(3)
①若小玲摸到$A$棋，$A$棋胜$B$棋、$C$棋，$B$棋有$2$枚，$C$棋有$3$枚，共$2 + 3=5$枚，小玲胜小军的概率$P_1=\frac{5}{9}$。
②若小玲摸到$B$棋，$B$棋胜$C$棋、$D$棋，$C$棋有$3$枚，$D$棋有$4$枚，共$3 + 4 = 7$枚，小玲胜小军的概率$P_2=\frac{7}{9}$。
③若小玲摸到$C$棋，由
(2)知$P_3=\frac{4}{9}$。
④若小玲摸到$D$棋，$D$棋胜$A$棋，$A$棋有$1$枚，小玲胜小军的概率$P_4=\frac{1}{9}$。
因为$\frac{7}{9}＞\frac{5}{9}＞\frac{4}{9}＞\frac{1}{9}$，所以小玲摸到$B$棋使她胜小军的概率最大。
综上，答案依次为：
(1)$\frac{3}{10}$；
(2)$\frac{4}{9}$；
(3)$B$棋。