《2025年同步测控优化设计七年级数学上册人教版》

1. 配套问题
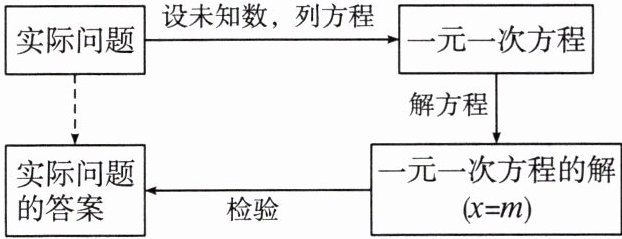
这类问题中配套的物品之间具有一定的数量关系,这可以作为列方程的依据。
2. 工程问题
这类问题中常常把总工作量看作 1,并利用“工作量 = 人均效率 × 人数 × 时间”的关系考虑问题。
3. 用一元一次方程解决实际问题的基本过程

答案： 人均效率 人数 时间

1. 配套问题
典例 1 工厂某车间制作一批机器部件,一个机器部件由 2 个 A 零件和 4 个 B 零件组成。若制作一个 A 零件需用 0.05 kg 铝料,制作一个 B 零件需用 0.02 kg 铝料。现共有铝料 4500 kg,求最多能制作出机器部件的数量。

答案： 答：设最多能制作出机器部件$x$个。
每个机器部件需要$2$个A零件和$4$个B零件。
制作一个A零件需要$0.05$ kg铝料，制作一个B零件需要$0.02$ kg铝料。
则每个机器部件需要的铝料总量为：
$2 × 0.05 + 4 × 0.02 = 0.1 + 0.08 = 0.18 kg$
共有铝料$4500$ kg，因此可以列出不等式：
$0.18x \leq 4500$
解这个不等式，得到：
$x \leq \frac{4500}{0.18}$
$x \leq 25000$
故最多能制作出机器部件$25000$个。