第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
5. 如图,在编写数学谜题时,“$\boxed{}$”内要求填写同一个数字,若设“$\boxed{}$”内的数字为$y$,则可列出方程
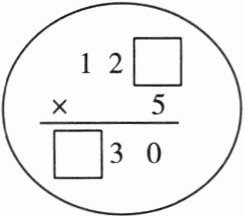
5(120+y)=100y+30
。
答案:
5(120+y)=100y+30
1. 方程的解和解方程
一般地,使方程左、右两边的值相等的
2. 一元一次方程的概念
一般地,如果方程中只含有
一般地,使方程左、右两边的值相等的
未知数
的值,叫作方程的解. 求方程的解的过程,叫作解方程.2. 一元一次方程的概念
一般地,如果方程中只含有
一
个未知数(元),且含有未知数的式子都是整式,未知数的次数都是1
,这样的方程叫作一元一次方程.
答案:
1. 未知数 2. 一 1
1. 了解方程的解和解方程的概念
典例1 观察下表,写出关于$x的方程2x + 1 = ax - 2$的解:
| $x$ | …$$ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | …$$ |
| $2x + 1$ | …$$ | $-5$ | $-3$ | $-1$ | $1$ | $3$ | $5$ | …$$ |
| $ax - 2$ | …$$ | $-\frac{7}{2}$ | $-3$ | $-\frac{5}{2}$ | $-2$ | $-\frac{3}{2}$ | $-1$ | …$$ |
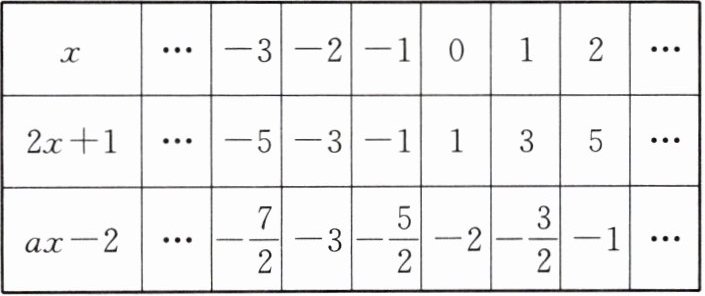
典例1 观察下表,写出关于$x的方程2x + 1 = ax - 2$的解:
$x = -2$
.| $x$ | …$$ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | …$$ |
| $2x + 1$ | …$$ | $-5$ | $-3$ | $-1$ | $1$ | $3$ | $5$ | …$$ |
| $ax - 2$ | …$$ | $-\frac{7}{2}$ | $-3$ | $-\frac{5}{2}$ | $-2$ | $-\frac{3}{2}$ | $-1$ | …$$ |

答案:
由表格可知,当$x = -2$时,$2x + 1 = -3$,$ax - 2 = -3$,此时$2x + 1 = ax - 2$。
所以关于$x$的方程$2x + 1 = ax - 2$的解为$x = -2$。
故答案为$x = -2$。
所以关于$x$的方程$2x + 1 = ax - 2$的解为$x = -2$。
故答案为$x = -2$。
举一反三 已知$x = 1是方程ax - b = 0$的解,则$2a - 2b + 2025 = $
2025
.
答案:
2025
2. 检验一个数是不是方程的解
典例2 判断$x = 3和x = 2是不是方程4x + 5 = 8x - 3$的解.
典例2 判断$x = 3和x = 2是不是方程4x + 5 = 8x - 3$的解.
答案:
检验$x=3$是否为方程的解:
将$x=3$代入方程左边:$4×3 + 5 = 12 + 5 = 17$
将$x=3$代入方程右边:$8×3 - 3 = 24 - 3 = 21$
因为$17\neq21$,所以$x=3$不是方程的解。
检验$x=2$是否为方程的解:
将$x=2$代入方程左边:$4×2 + 5 = 8 + 5 = 13$
将$x=2$代入方程右边:$8×2 - 3 = 16 - 3 = 13$
因为$13=13$,所以$x=2$是方程的解。
结论:$x=3$不是方程的解,$x=2$是方程的解。
将$x=3$代入方程左边:$4×3 + 5 = 12 + 5 = 17$
将$x=3$代入方程右边:$8×3 - 3 = 24 - 3 = 21$
因为$17\neq21$,所以$x=3$不是方程的解。
检验$x=2$是否为方程的解:
将$x=2$代入方程左边:$4×2 + 5 = 8 + 5 = 13$
将$x=2$代入方程右边:$8×2 - 3 = 16 - 3 = 13$
因为$13=13$,所以$x=2$是方程的解。
结论:$x=3$不是方程的解,$x=2$是方程的解。
举一反三 $x = 1$是方程
①$2 - x = 1$;②$2x = 2$;③$x + 2 = 3$;④$\frac{3x}{2} = 1$.
①②③
的解. (请填写所有符合条件的方程的序号)①$2 - x = 1$;②$2x = 2$;③$x + 2 = 3$;④$\frac{3x}{2} = 1$.
答案:
①②③
查看更多完整答案,请扫码查看


