《2025年同步测控优化设计七年级数学上册人教版》

典例某中学图书馆的窗户形状如图所示(单位:cm),其上部是半圆形,下部是 4 个相同的长方形,已知每个长方形的长为 a cm,宽为 b cm.

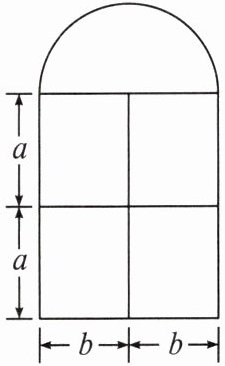
(1)列式表示窗户的面积;
(2)若 $ a = 80,b = 60 $,求窗户的面积(计算结果保留 π).
规律总结 常见的图形面积公式和体积公式有哪些?
$ S_{长方形} = ab $ (a 表示长,b 表示宽).
$ S_{正方形} = a^{2} $ (a 表示边长).
$ S_{三角形} = \frac{1}{2}ah $ (a 表示底,h 表示底 a 上的高).
$ S_{梯形} = \frac{1}{2}(a + b) \cdot h $ (a 表示上底,b 表示下底,h 表示高).
$ S_{圆} = \pi r^{2} $ (r 表示半径).
$ V_{长方体} = abh $ (a 表示长,b 表示宽,h 表示高).
$ V_{正方体} = a^{3} $ (a 表示棱长).

答案：
(1) $4ab + \frac{1}{2}\pi b^2$；
(2) $19200 + 1800\pi$。

举一反三 “文房四宝”中砚台的示意图如图所示. 砚台外部的正方形边长为 m,内部圆形凹槽半径为 n.

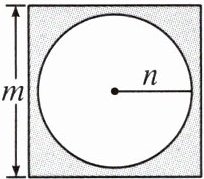
(1)用含有 m,n 的式子表示这个砚台阴影部分的面积 $ S = $$m^{2}-\pi n^{2}$;
(2)当 $ m = 14,n = 6 $ 时, $ S = $88. (π 取 3)

答案：
(1)$m^{2}-\pi n^{2}$
(2)88 解析
(1)由题意可得这个砚台阴影部分的面积$S=m^{2}-\pi n^{2}$.
(2)当$m=14$,$n=6$时,$S=14^{2}-3×6^{2}=88$.

1. 如图,若 $ a = 10,b = 4 $,则这个图形的面积是( )


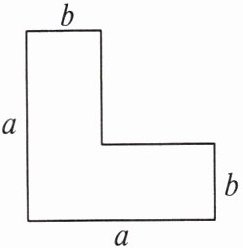
A.32
B.42
C.80
D.64

答案：
D 解析 如图所示， 白色部分图形的面积为$a^{2}-(a-b)^{2}$.当$a=10$,$b=4$时,$a^{2}-(a-b)^{2}=10^{2}-(10-4)^{2}=64$.

2. 若 a,b 分别表示长方形的长和宽,则
(1)长方形的周长 $ l = $2a+2b,面积 $ S = $ab;
(2)当 $ a = 2cm,b = 3cm $ 时,周长 $ l = $10cm,面积 $ S = $6 $ cm^{2} $.

答案：
(1)$2a+2b$ $ab$
(2)10 6