《2025年同步测控优化设计七年级数学上册人教版》

1. 某县去年城镇居民人均可支配收入为x万元,与前年相比增长y%,则该县前年城镇居民人均可支配收入为(D)万元.
A.$x(1 - y\%)$
B.$x(1 + y\%)$
C.$\frac{x}{1 - y\%}$
D.$\frac{x}{1 + y\%}$

答案： D

2. 购买2束单价为m元的百合花和3束单价为n元的洋兰,需要2m+3n元.

答案： 2m+3n

3. 用代数式表示：
(1)比x的3倍小2的数；
(2)a的$\frac{4}{7}$与b的$\frac{1}{5}$的和；
(3)比m与n的差的平方大6的数.

答案： 解
(1)3x-2;
(2)$\frac{4}{7}a+\frac{1}{5}b$;
(3)$(m-n)^2+6$.

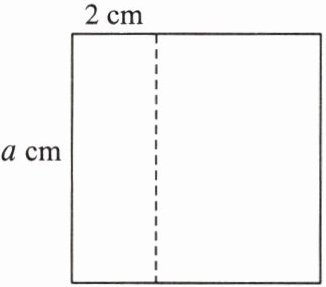
4. 如图,从一张边长为a cm($a ＞ 2$)的正方形铁皮上截去一个2 cm宽的长方形铁皮,则剩余$(a^2-2a)$$cm^2$的铁皮.

答案： $(a^2-2a)$

5. 某商场销售一种上衣,进价为x元/件,先按进价的2倍作为定价,而实际销售时按定价打八折出售.
试用代数式表示：
(1)每件上衣最初的定价为2x元；
(2)每件上衣打八折后的销售价为1.6x元；
(3)n件上衣打八折后的利润为0.6xn元.

答案：
(1)2x
(2)1.6x
(3)0.6xn

反比例关系
(1)一般地,对于工程问题,当工作效率保持不变,工作量与工作时间是成正比例的量,它们成正比例关系。
(2)两个相关联的量,一个量变化,另一个量也随着变化,且这两个量的乘积一定,这两个量就叫作成反比例的量,它们之间的关系叫作反比例关系。
(3)如果用字母$x和y$表示两个相关联的量,用$k$表示它们的积($k$是一个确定的值,且$k\ne0$),反比例关系可以用$xy = k$来表示。

答案：
(1)正比例 正比例
(2)乘积 反比例关系