第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. 已知 $ |a| = 3 $,$ |b| = 5 $,且 $ a > 0 $,$ b > 0 $,求 $ a + b $ 的值.
答案:
解 因为|a|=3,|b|=5,所以a=±3,b=±5. 因为a>0,b>0,所以a=3,b=5. 所以a+b=3+5=8.
8. 若 $ |x - 4| = 0 $,$ y $ 是 $ - 3 $ 的相反数,求 $ x - y $ 的值.
答案:
解 因为|x-4|=0,所以x-4=0,所以x=4. 因为y是-3的相反数,所以y=3. 所以x-y=4-3=1.
1. 用数轴比较有理数的大小
在正方向向右的数轴上表示有理数,它们从左到右的顺序,就是
2. 用法则比较有理数的大小
一般地,(1)正数
(2)两个负数,绝对值大的
在正方向向右的数轴上表示有理数,它们从左到右的顺序,就是
从小到大
的顺序,即左边的数小于
右边的数。2. 用法则比较有理数的大小
一般地,(1)正数
大于
0,0大于
负数,正数大于
负数;(2)两个负数,绝对值大的
反而小
。
答案:
1. 从小到大 小于;2.
(1)大于 大于 大于;
(2)反而小
(1)大于 大于 大于;
(2)反而小
1. 用数轴比较有理数的大小
典例1 在数轴上表示下面各数,并将这些数按从小到大的顺序排列,用“<”连接起来:
-2.5,-(-$\frac{3}{2}$),0,$\frac{2}{3}$,-|-2|,+(-1.5)。
规律总结 利用数轴比较有理数的大小,先在数轴上表示各数,再利用正方向和位置关系比较大小。
举一反三 表示有理数$a$,$b$的点在数轴上的位置如图所示,下列结论正确的是(
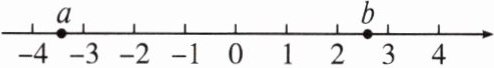
A.$a > -3$
B.$b > 3$
C.$a > b$
D.$-a > b$
典例1 在数轴上表示下面各数,并将这些数按从小到大的顺序排列,用“<”连接起来:
-2.5,-(-$\frac{3}{2}$),0,$\frac{2}{3}$,-|-2|,+(-1.5)。
规律总结 利用数轴比较有理数的大小,先在数轴上表示各数,再利用正方向和位置关系比较大小。
举一反三 表示有理数$a$,$b$的点在数轴上的位置如图所示,下列结论正确的是(
D
)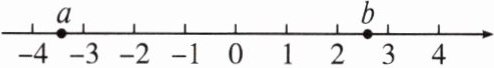
A.$a > -3$
B.$b > 3$
C.$a > b$
D.$-a > b$
答案:
D
2. 用法则比较有理数的大小
典例2 下表是我国几个城市某年1月份的平均气温,在这些城市中,平均气温最低的城市是(

A. 北京
B. 沈阳
C. 广州
D. 太原
规律总结 如何用法则比较两数的大小?
(1)两数 $\begin{cases} 同为正号:绝对值大的数大 \\ 同为负号:绝对值大的反而小 \end{cases} $
(2)两数异号:正数大于负数
(3)一数为0 $\begin{cases} 正数与0:正数大于0 \\ 负数与0:负数小于0 \end{cases} $
举一反三 比较大小:
(1)$-\frac{3}{4}$
(2)$-(-2)$
典例2 下表是我国几个城市某年1月份的平均气温,在这些城市中,平均气温最低的城市是(
B
)
A. 北京
B. 沈阳
C. 广州
D. 太原
规律总结 如何用法则比较两数的大小?
(1)两数 $\begin{cases} 同为正号:绝对值大的数大 \\ 同为负号:绝对值大的反而小 \end{cases} $
(2)两数异号:正数大于负数
(3)一数为0 $\begin{cases} 正数与0:正数大于0 \\ 负数与0:负数小于0 \end{cases} $
举一反三 比较大小:
(1)$-\frac{3}{4}$
>
$-\frac{4}{5}$;(2)$-(-2)$
>
$-|-2.01|$。
答案:
B
(1)>
(2)>
(1)>
(2)>
查看更多完整答案,请扫码查看


