《2025年全效学习同步学练测七年级数学上册湘教版》

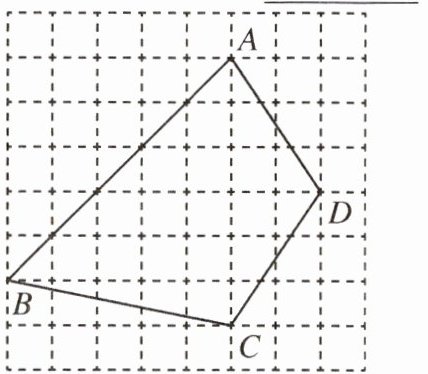
8. 我们在计算不规则图形的面积时，有时采用“方格法”来计算，计算方法如下：假定每个小方格的边长为 1，$ S $ 为图形的面积，$ L $ 是图形边界上的格点数，$ N $ 是图形内部格点数，则有 $ S = \frac{L}{2} + N - 1 $，请根据此方法计算图中四边形 $ ABCD $ 的面积 $ S = $21。

答案： 8.21

9. 研究表明，运动时心跳速率通常和人的年龄有关。若用 $ a $ 表示一个人的年龄，用 $ b $ 表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，则 $ b = 0.8(220 - a) $。
（1）正常情况下，一个 14 岁的少年运动时所能承受的每分钟心跳的最高次数是多少？
（2）一个 45 岁的人运动时，每分钟心跳次数为 132 次，请问他有危险吗？为什么？

答案： $(1)$计算$14$岁少年运动时所能承受的每分钟心跳的最高次数
解：已知$b = 0.8(220 - a)$，当$a = 14$时，将$a = 14$代入公式$b = 0.8(220 - a)$中，可得：
$b=0.8×(220 - 14)$
$=0.8×206$
$ = 164.8$（次）
$(2)$判断$45$岁的人运动时每分钟心跳$132$次是否有危险
解：当$a = 45$时，代入$b = 0.8(220 - a)$，可得：
$b=0.8×(220 - 45)$
$=0.8×175$
$= 140$（次）
因为$132\lt140$，即这个人运动时每分钟心跳次数$132$次小于他这个年龄所能承受的每分钟心跳的最高次数$140$次。
所以，$(1)$ $14$岁少年运动时所能承受的每分钟心跳的最高次数是$164.8$次；$(2)$ 他没有危险，因为$45$岁的人运动时所能承受的每分钟心跳的最高次数是$140$次，$132\lt140$。

10. 王刚同学每天乘坐地铁上学，为了方便乘坐地铁，他买了 150 元的城市卡。如果他乘坐地铁的次数用 $ x $ 表示，则记录他每次乘坐地铁后城市卡的余额（单位：元）如下表：

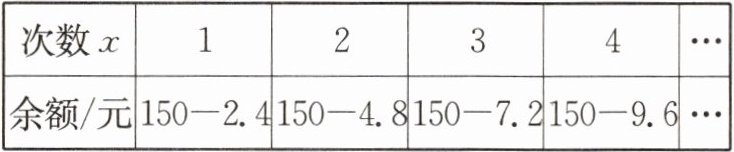
（1）写出用 $ x $ 表示余额的代数式。
（2）利用（1）中的式子，帮助王刚同学算一算如果他一个月乘坐地铁 42 次，这 150 元的城市卡够不够用？若够用，能剩多少元？

答案： 10.
(1)乘坐地铁x次后的余额为(150 - 2.4x)元
(2)够用，能剩49.2元

11. [2024 河南模拟]如图，四边形 $ ABCD $ 是一个长方形。
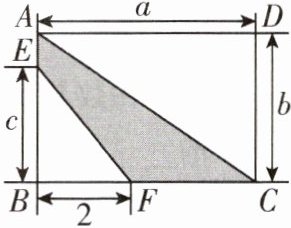
（1）根据图中数据，用含 $ a $，$ b $，$ c $ 的代数式表示图中阴影部分的面积 $ S $；
（2）当 $ a = 5 $，$ b = 4 $，$ c = 3 $ 时，求 $ S $ 的值。

答案： $11.(1)S_{阴影}=\frac{1}{2}ab - c (2)S = 7$

12. 【应用意识】某服装厂生产一种西装和领带，每套西装定价 400 元，每条领带定价 50 元。厂方在开展促销活动期间，向客户提供两种优惠方案：
方案①：买一套西装送一条领带；
方案②：西装和领带都按定价的 90%付款。
现某客户要到该服装厂购买西装 20 套，领带 $ x $ 条（$ x ＞ 20 $）。
（1）若该客户按方案①购买，需付款______元（用含 $ x $ 的代数式表示）；若该客户按方案②购买，需付款______元（用含 $ x $ 的代数式表示）。
（2）若 $ x = 30 $，通过计算说明此时按哪种方案购买较为合算。
（3）若两种优惠方案可同时使用，当 $ x = 30 $ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法并计算出此种方案的付款金额。

答案： 12.
(1)(7000 + 50x) (45x + 7200)
(2)此时按方案①购买较为合算
(3)能.用方案①买20套西装送20条领带，再用方案②买10条领带.总价钱为8450(元)